書籍「アートで魅せる数学の世界」のp.9-56で紹介されている黄金比に関連する図形について再現を試みています。
黄金比とは
下図のような、短辺の長さが\(1\)、長辺の長さが\(\varphi\)である長方形(黒色)を考えます。
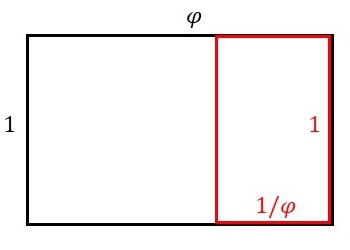
この長方形から、辺の長さが\(1\)の正方形部分を取り除きます。このとき、残った部分の長方形(赤色)が元の長方形(黒色)と相似になるとき、長方形の縦と横の長さの比を黄金比(Golden ratio)と呼びます。
なお、黄金比の値\(\varphi\)は、\[ 1-\varphi = \frac{1}{\varphi} \ \ \to \ \ \varphi = \frac{1+\sqrt{5}}{2} \]で与えられます。
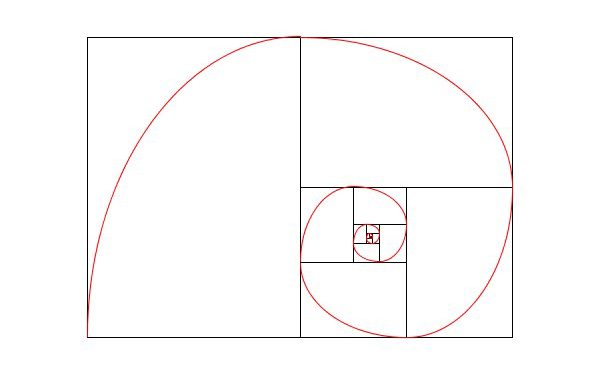
黄金比による螺旋
書籍「アートで魅せる数学の世界」のp.12で紹介されている黄金比を用いた疑似的な螺旋の再現を試みています。
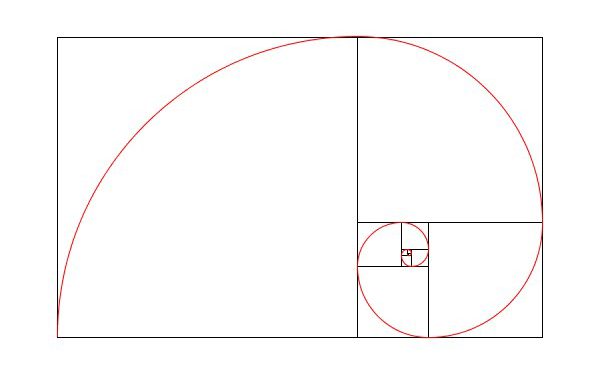
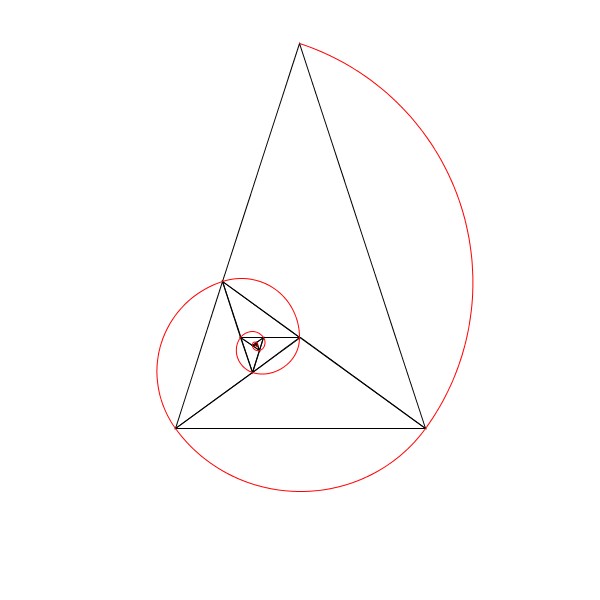
黄金三角形
書籍「アートで魅せる数学の世界」のp.22-26で紹介されている黄金三角形に関連する図形について再現を試みています。

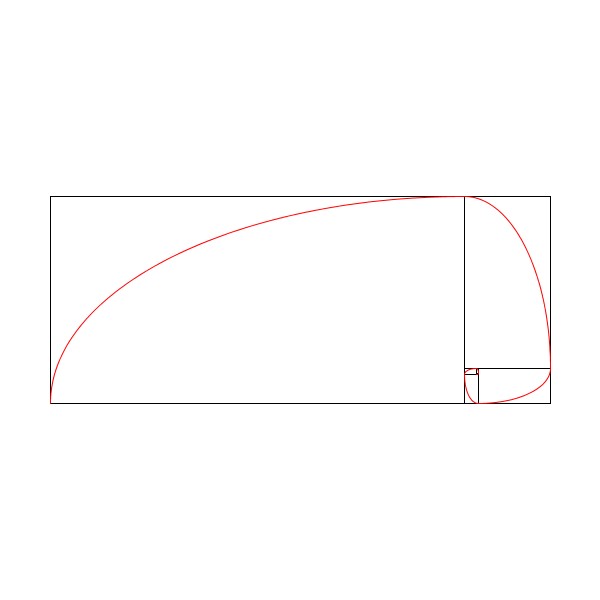
白銀比による螺旋
書籍「アートで魅せる数学の世界」のp.19で紹介されている白銀比を用いて、黄金比の時と同様に疑似的な螺旋を描いてみました。
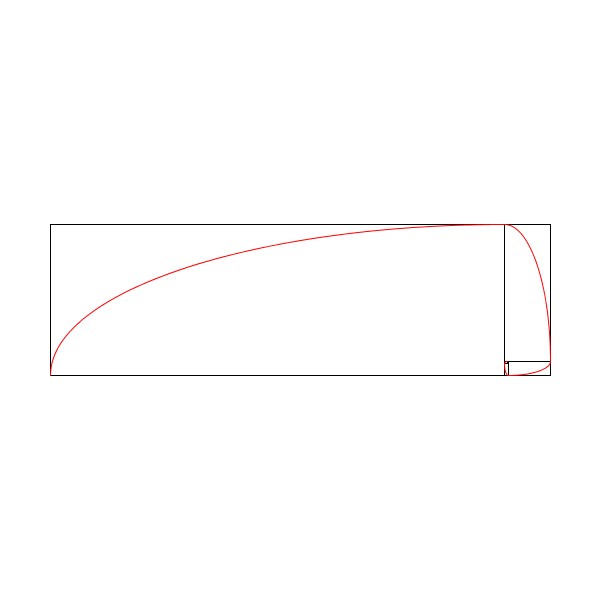
貴金属比による螺旋
書籍「アートで魅せる数学の世界」のp.19-21で紹介されている貴金属比を用いた疑似的な螺旋の再現を試みています。
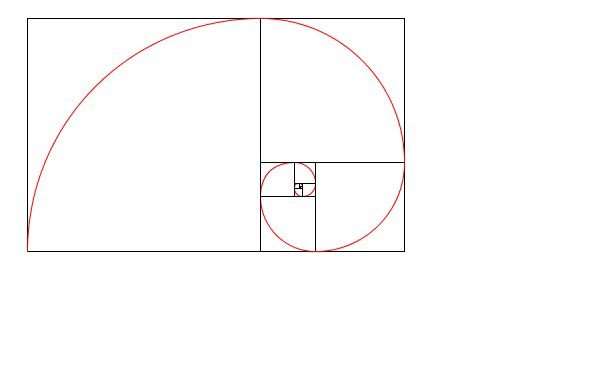
フィボナッチ数列による螺旋
書籍「アートで魅せる数学の世界」のp.30-31で、フィボナッチ数を用いたフィボナッチ長方形が紹介されています。今回はこれに疑似的な螺旋を乗せてみました。
ゼッケンドルフ表現
書籍「アートで魅せる数学の世界」のp.41-43で、フィボナッチ数に関する定理「ゼッケンドルフの定理」を用いた図形が紹介されています。今回はこれを再現してみました。