書籍「アートで魅せる数学の世界」のp.30-31で、フィボナッチ数を用いたフィボナッチ長方形が紹介されています。今回はこれに疑似的な螺旋を乗せてみました。
フィボナッチ数列
フィボナッチ数列とは、以下のような数列です。\[ 0, \ \ 1, \ \ 1, \ \ 2, \ \ 3, \ \ 5, \ \ 8, \ \ 13, \ \ 21, \ \ 34, \ \ 55, \ \ 89, \ \ 144, \ \ \cdots \]特徴として、ある数はその前の2つの数の和になっています。
フィボナッチ数列と黄金比
フィボナッチ数列と黄金比との関係を見てみます。\(n\)番目のフィボナッチ数を\(F_n\)で表すと、フィボナッチ数列の漸化式は\[F_n = F_{n-1}+F_{n-2}, \ \ F_0 = 0, \ \ F_1 = 1 \]で表されます。この漸化式からフィボナッチ数\(F_n\)は\[ F_n = \frac{ \varphi_+^n – \varphi_-^n }{ \varphi_+ – \varphi_- } \]と表すことができます。ここで、\[ \varphi_{\pm} = \frac{ 1 \pm \sqrt{5} }{2} \]です。\(\varphi_+\)はまさに黄金比の値です。
さらに、フィボナッチ数列の連続した2つの値\(F_{n-1}\)と\(F_n\)との比を見てみると、\[ \frac{F_n}{F_{n-1}} = \frac{ \varphi_+^n – \varphi_-^n }{ \varphi_+^{n-1} – \varphi_-^{n-1} } = \varphi_+ \frac{ 1 – (-1)^n \varphi_-^{2n} }{ 1 – (-1)^{n-1} \varphi_-^{2(n-1)} } \underset{n \to \infty}{\longrightarrow} \varphi_+ \]のようになります。これは、フィボナッチ数列の連続した2つの値の比がだんだん黄金比に近づいていくことを表しています。
フィボナッチ数列による螺旋
今回作成したフィボナッチ数列による螺旋は以下のような図形になります。
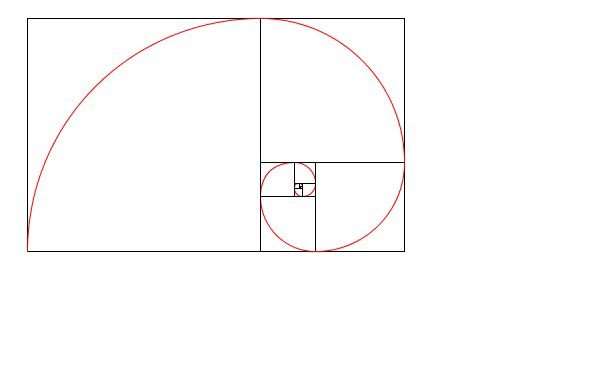
書籍「アートで魅せる数学の世界」のp.30-31で解説されているフィボナッチ数列の値を辺の長さとする正方形を準備に並べていったものに合わせて円弧を描いていくことで、疑似的な螺旋を描いています。
ソースコード
このフィボナッチ数列を用いた疑似的な螺旋を描くプログラムのソースコードを示しておきます。
void setup(){
size(600,600);
background(255,255,255);
translate(width/2.0, height/2.0);
noFill();
// 3つのフィボナッチ数列
int fibo0 = 0;
int fibo1 = 1;
int fibo2 = 1;
PVector center = new PVector(0.0,0.0); // 扇形の中心位置
PVector direction = new PVector(1.0, 0.0); // 中心位置を移動する際の基準ベクトル
float theta = radians(270.0); // 中心位置を移動させる角度
PVector opposite = center.copy().add( direction.copy().mult(sqrt(2.0)*fibo1).rotate(theta - radians(45.0)) ); // 正方形の反対の位置座標
int count = 0;
rectMode(CORNERS);
while( fibo1 < 300 ){
stroke(0,0,0);
rect(center.x, center.y, opposite.x, opposite.y);
stroke(255,0,0);
arc(center.x, center.y, 2.0*fibo1, 2.0*fibo1, theta - radians(90.0), theta);
// 中心位置を更新
center.add( direction.copy().mult(fibo0).rotate(theta + radians(90.0)) );
// フィボナッチ数列を更新
fibo0 = fibo1;
fibo1 = fibo2;
fibo2 = fibo0 + fibo1;
// 移動方向などを更新
count++;
theta = radians(270.0) - radians(90.0) * (count%4);
opposite = center.copy().add( direction.copy().mult(sqrt(2.0)*fibo1).rotate(theta - radians(45.0)) );
}
}