書籍「アートで魅せる数学の世界」のp.19で紹介されている白銀比を用いて、黄金比の時と同様に疑似的な螺旋を描いてみました。
Contents
白銀比とは
下図のような、短辺の長さが\(1\)、長辺の長さが\(\sqrt{2}\)である長方形(黒色)を考えます。
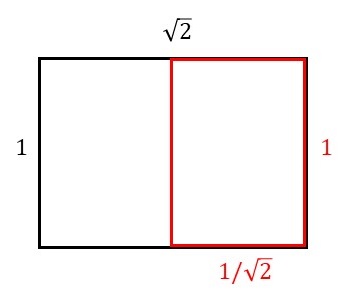
この長方形の長辺を2等分することで、2つの同じ大きさの長方形に分割することができます。このようにして分割された長方形(赤色)はもとの長方形(黒色)と相似になります。このような長方形の縦と横の長さの比を白銀比(Silver ratio)と呼び、\(1:\sqrt{2}\)となります。
なお、この白銀比は、日常的によく使われているものです。ノートのサイズで「A4サイズ」とか「B5サイズ」とか聞いたことがあると思います。面積が\(1\mathrm{m}^2\)となるような白銀比を持つ長方形を「A0サイズ」として、これを半分にしていくことで「A1サイズ」「A2サイズ」とA版サイズが決まっていきます。また、面積が\(1.5\mathrm{m}^2\)となるような白銀比を持つ長方形を「B0サイズ」とすることで、同様にB版サイズが決まっていきます。
白銀比による螺旋
今回作成した白銀比による螺旋は以下のような図形になります。
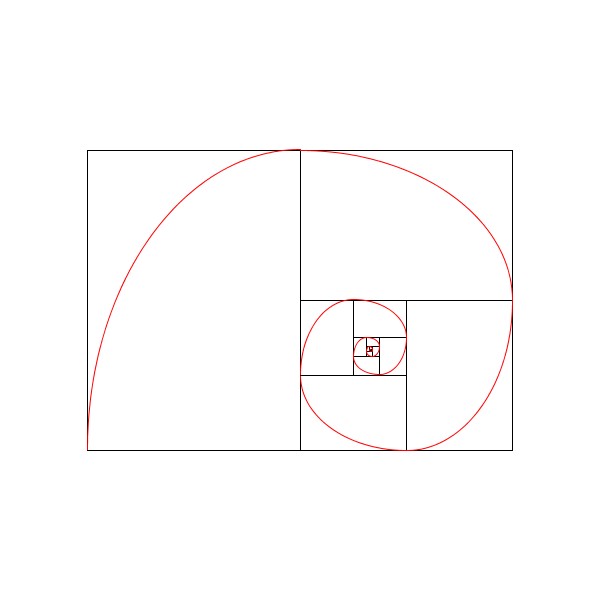
この図形は、白銀比をもつ長方形を、2つの長方形に順に分割したものに合わせて、長方形の辺の短辺と長辺の長さをそれぞれ短半径と長半径とした楕円の円弧を描くことで作成することができます。なお、円弧をつないだものですので、実際の螺旋とはことなります。そのため、疑似的な螺旋としています。
ソースコード
この白銀比を用いた疑似的な螺旋を描くプログラムのソースコードを示しておきます。
void setup(){
size(600,600);
background(255,255,255);
noFill();
float phi = sqrt(2.0); // 黄金比
float len = 300.0; // 一番大きい長方形の短辺の長さ
translate(width/2.0 + len*phi/2.0, height/2.0 + len/2.0);
PVector center = new PVector(0.0,0.0); // 扇形の中心位置
PVector opposite = new PVector(0.0,0.0); // 長方形の対角線上の中心位置と反対の点の座標
PVector direction = new PVector(1.0, 0.0); // 反対の点の位置を決めるための基準となるベクトル
int count = 0;
float theta;
rectMode(CORNERS);
while( len > 1.0 ){
theta = radians(90.0) * ((count+2)%4);
center.add( direction.copy().mult(len/phi).rotate(theta) );
opposite = center.copy().add( direction.copy().mult(sqrt(3.0/2.0)*len).rotate(theta + atan(sqrt(2.0))) );
stroke(0,0,0);
rect(center.x, center.y, opposite.x, opposite.y);
stroke(255,0,0);
if(count%2 == 0){
arc(center.x, center.y, 2.0*len / phi, 2.0*len, theta, theta + radians(90.0));
} else {
arc(center.x, center.y, 2.0*len, 2.0*len / phi, theta, theta + radians(90.0));
}
len *= 1.0/phi;
count++;
}
}