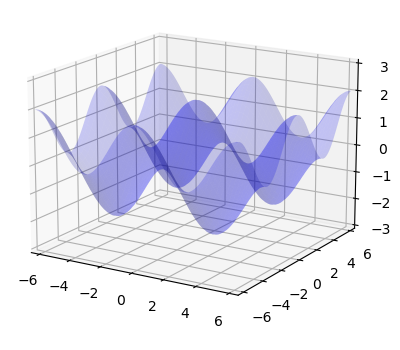
記事「たまごパック」をサイトにアップしました。以下のようなたまごパック形状をランダムドット・ステレオグラムで表現しています。
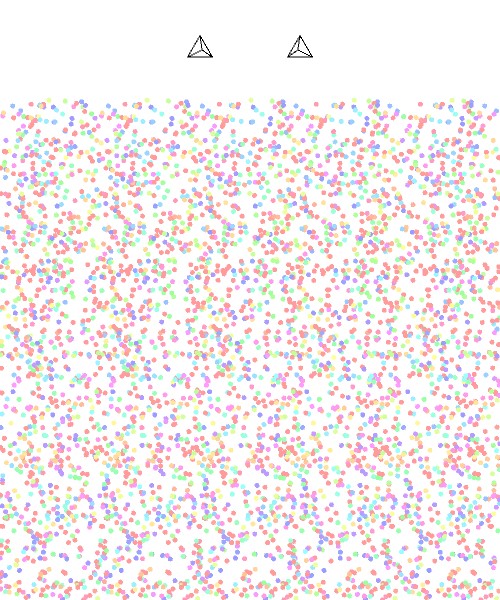
このランダムドット・ステレオグラムの見方ですが、まずランダムドット・ステレオグラムを紙に印刷してください。そして、その紙を少しずつ自分の目に近づけていってください。そうすると、上部の2つの図形が3つに見えるようになってきます。そのあたりで紙の位置を前後に微調整しながら、さらに根気強くピントを合わせていくと、3つに見える図形のうち、真ん中の図形が正四面体の形で飛び出て見えるようになります。このとき、下の点の集まりの中にぼんやりと何かが浮かび上がってきます。うまく下の図形に視線を移すことができれば、その浮かび上がってきた図形が何かわかるはずです。
今回たまごパック形状のランダムドット・ステレオグラムを紹介したわけですが、前回紹介したバウムクーヘン形状のランダムドット・ステレオグラムとその作成方法はほとんど変わりませんでした。違いはたまごパック形状を表す方程式が\(z=A(\cos \alpha x + \cos \alpha y) \)であるのに対し、バウムクーヘン形状を表す方程式が\(z=A \cos \alpha \sqrt{x^2+y^2} \)であることだけ。実際、記事「たまごパック」と「バウムクーヘン」はほとんど同じことが書いてあります。
ただ、実は一つ気になったことが・・・。それは、視線と立体形状との交点を求めるところで利用しているニュートン法のことです。たまごパック形状に対して\(A\)と\(\alpha\)の値をうまく取らないとニュートン法での処理が収束しないようです。確かに、たまごパック形状は極値がたくさん出てくるので、ニュートン法がうまく動くかは初期値の選び方にかなり左右されそうというのはなんとなくわかる。
こういう場合って一般にどうするのでしょうかね。初期値をうまく選ぶ方法がある?極値がたくさんある場合にニュートン法にかわる別の良い方法がある?
方程式の解を数値的に求めるという初歩的な処理でも奥深いものがあるなと感じました。