基本図形の形を考える

別記事「渦巻き図形」で、17種類の壁紙群について渦巻き状の模様を描いた図形を並べて壁紙アートの例を解説しました。その際、それぞれの基本図形の形は格子形状や対称性に合わせて、直観的に選んでいました。実際は、基本図形の形状をもう少しバラエティ豊かに選ぶことができます。

ここでは、基本図形の形状について考えてみたいと思います。

ボロノイ図を利用した分類

基本図形の形状について、今回はボロノイ図を用いて考えてみました。ボロノイ図とは平面上のいくつかの点（母点）を打ち、母点を一つだけ含む領域で、領域内の任意の点はその領域の母点が他の領域の母点よりも近くなるように分割した図になります。ボロノイ図についての詳細は別記事「ボロノイ図」で解説しています。

別記事「渦巻き図形」では、格子形状や対称性を考慮して基本図形の形を直観的に選び、基本図形を対称性に合わせて並べていくというやり方で行いました。ここでは、基本図形の部分を一つの点に変えて、この点を対称性に合わせて並べていきます。これらの並べた点を母点としてボロノイ図を作成します。すると、このボロノイ図はそれぞれの分割された領域を基本図形とした壁紙アートとなります。

なお、この記事は、書籍「エッシャー・マジック―だまし絵の世界を数理で読み解く」の5.1節（p.74~p.77）を参考にして考えています。

P1群の基本図形の形状

P1群のボロノイ図

まずP1群の対称性をもつ母点に対してボロノイ図を作ってみます。

P1群のベースとなる一般格子の形状（黒点）に対して、互いに近傍にある4つの一般格子点の中央に一つの点（白点）をとり、この点をP1群の対称性に合わせて並べていくと以下のような図になります。

これらの白点を母点としてボロノイ図を作成したものが以下の図になります。

この結果から、P1群の基本図形は六角形にできることが分かります。実際、この図形は基本図形の六角形の一般格子上での並進移動（P1群の対称性）に対して不変になっています。

P1群の基本図形への制約

ボロノイ図から得られたP1群の基本図形は六角形になりましたが、直観的に考えたときの基本図形が平行四辺形であったように、基本図形はボロノイ図から得られた六角形に限られるものではありません。ただ、ボロノイ図から得られた形状とP1群の対称性から、P1群の基本図形の形状に対していくつかの制約が見えてきます。

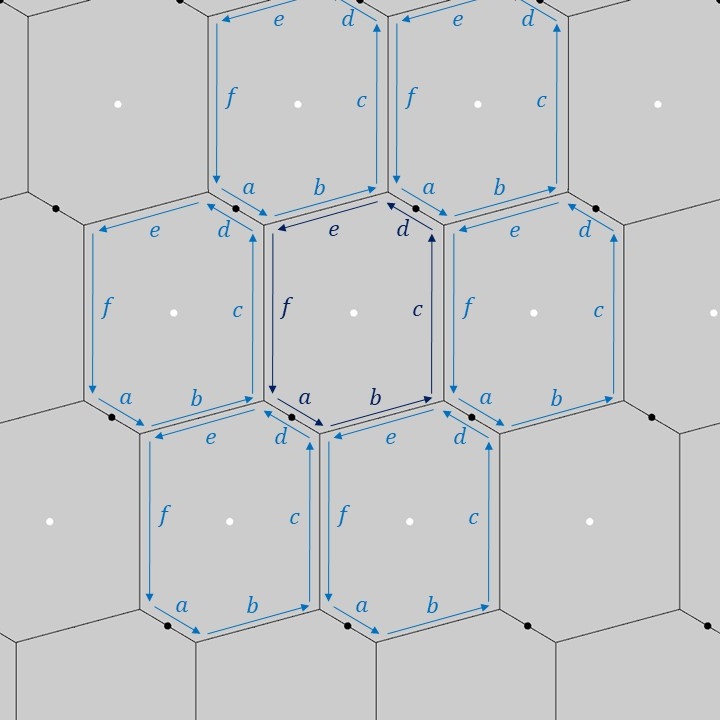
上図のように、中央に位置している基本図形の六角形の各辺に\(a,b,c,d,e,f\)のラベルを付けてみます（濃い青色のラベル）。この中央の図形を一般格子上で並進移動（P1群の対称性）させると、隣り合う六角形に対するラベルは薄い青色のラベルのようになります。隣り合う六角形同士の各辺の対応関係を見てみると、六角形の性質として、辺\(a\)と辺\(d\)、辺\(b\)と辺\(e\)、辺\(c\)と辺\(f\)がそれぞれ長さが等しく、互いに平行となっていることが分かります。つまり、これがP1群の基本図形に対する制約となっています。

なお、別記事「渦巻き図形」で直観的に選んだP1群の基本図形は平行四辺形でした。これは六角形に対して辺\(a\)と辺\(d\)がそれぞれ縮んでその中点に収束した場合と考えることができます。

P2群の基本図形の形状

P2群のボロノイ図

P2群の対称性をもつ母点に対してボロノイ図を作ってみます。

P2群のベースとなる一般格子の形状（黒点）に対して、互いに近傍にある4つの一般格子点のうち1つの点から平行四辺形の対角線方向に3分の1の長さの位置にある点（白点）をとり、この点をP2群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

この結果から、P2群の基本図形は六角形にできることが分かります。実際、下図に示す通り、この図形は一般格子上での並進移動および赤点を中心とした180°回転（P2群の対称性）に対して不変になっています。

P2群の基本図形への制約

P2群によるボロノイ図から、P2群の基本図形への制約について考えてみます。

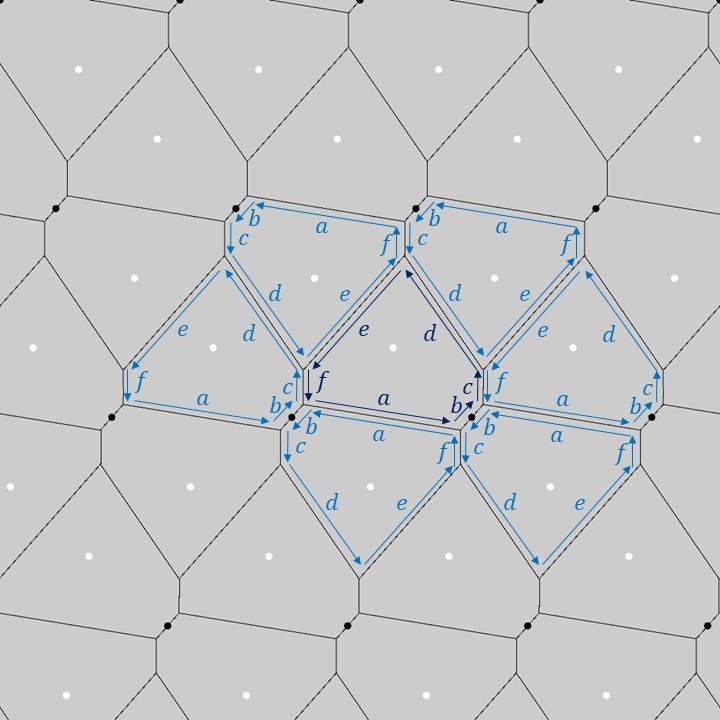
上図のように、1つの基本図形の六角形の各辺に\(a,b,c,d,e,f\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を一般格子上でP2群の対称性に合わせて移動させると、隣り合う六角形に対するラベルは薄い青色のラベルのようになります。隣り合う六角形同士の各辺の対応関係を見てみると、六角形の性質として、辺\(c\)と辺\(f\)の長さが等しく、互いに平行となっていて、それ以外の辺\(a,b,d,e\)は各辺の中点が180°回転中心となるように配置されることが分かります。また、辺\(b\)の中点は一般格子と一致しており、一方、辺\(a,d,e\)の中点は隣り合う一般格子同士の中点と一致しています。これがP2群の基本図形に対する制約となっています。

なお、別記事「渦巻き図形」で直観的に選んだP2群の基本図形は平行四辺形でした。これは六角形に対して、辺\(c\)が縮んでその中点に収束し、かつ辺\(d\)と辺\(e\)が互いに平行になった場合と考えることができます。

PM群の基本図形の形状

PM群のボロノイ図

PM群の対称性をもつ母点に対してボロノイ図を作ってみます。

PM群のベースとなる長方格子の形状（黒点）に対して、1つの長方格子点から横隣りの格子点までの距離の3分の1、下隣りの格子点までの距離の3分の1の長さまで移動した位置にある点（白点）をとり、この点をPM群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

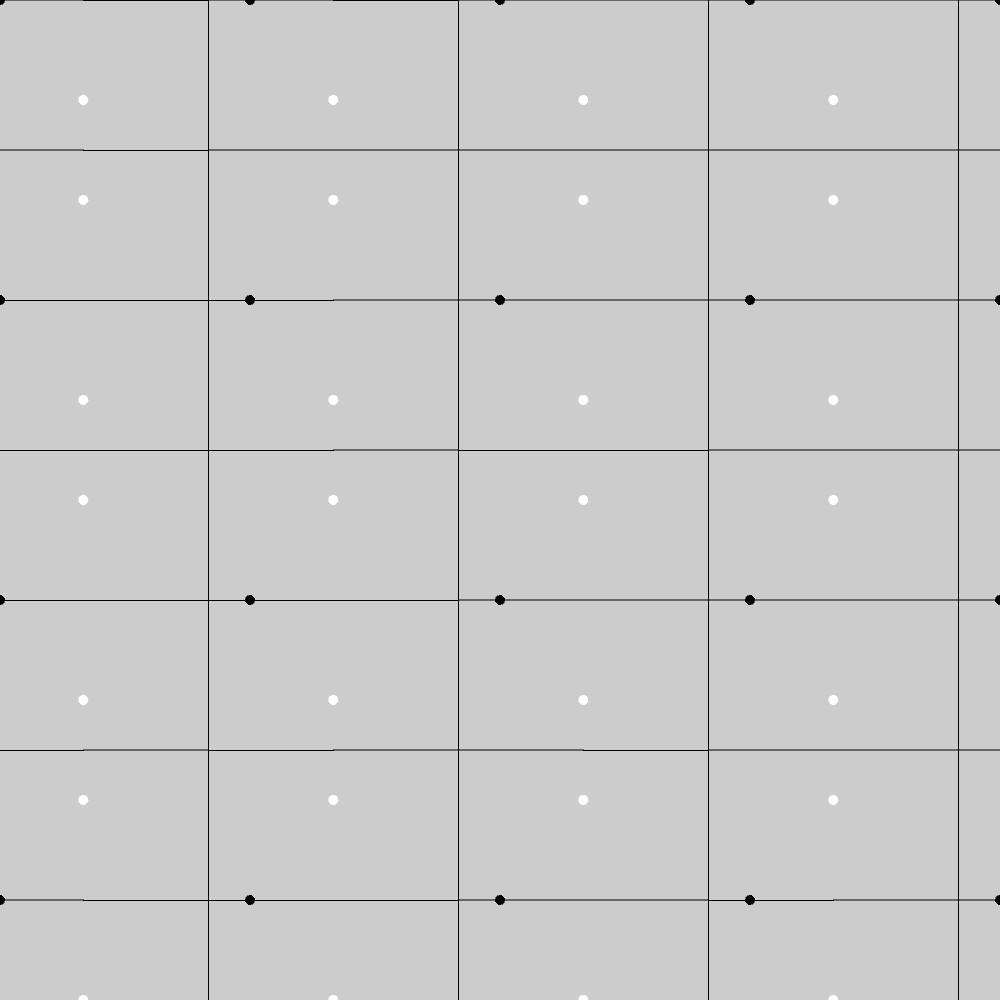
この結果から、PM群の基本図形は長方形になることが分かります。実際、下図に示す通り、この図形は長方格子上での一方向のみ（赤い線）の鏡映変換（PM群の対称性）に対して不変になっています。

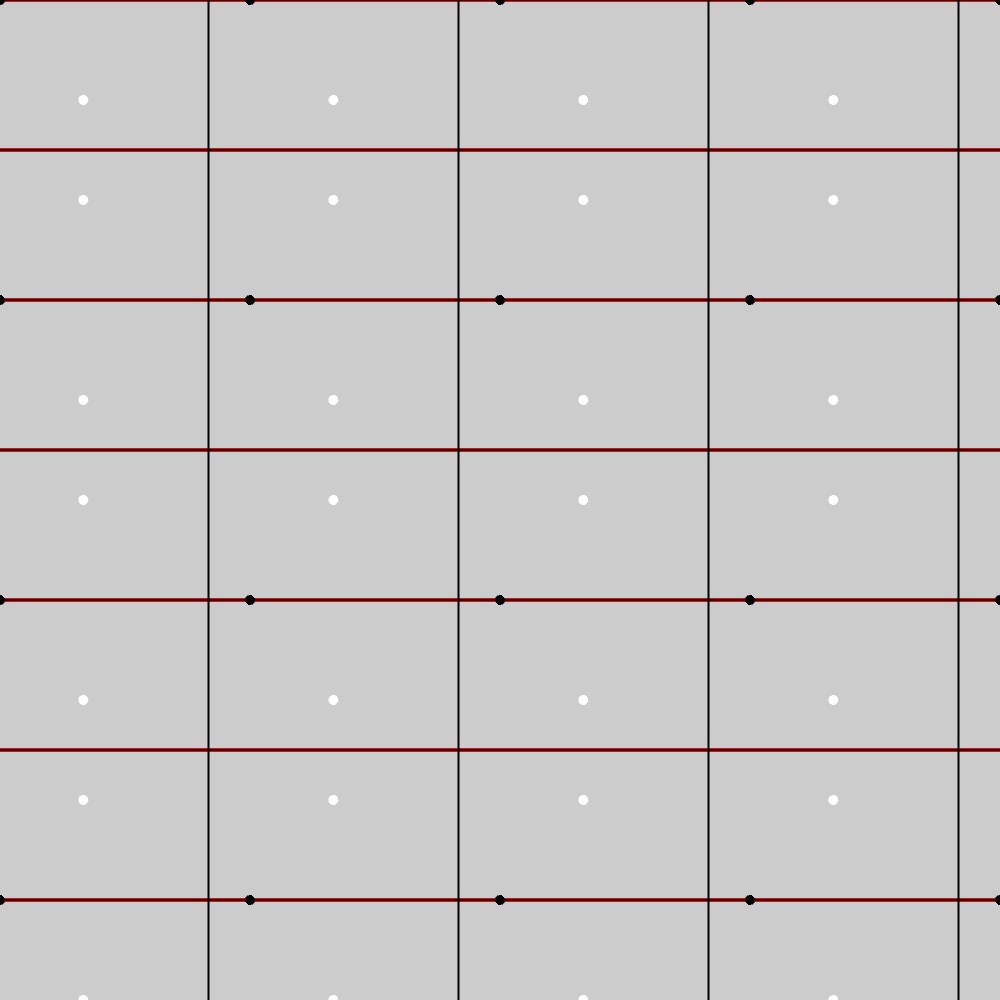
PM群の基本図形への制約

PM群によるボロノイ図から、PM群の基本図形への制約について考えてみます。

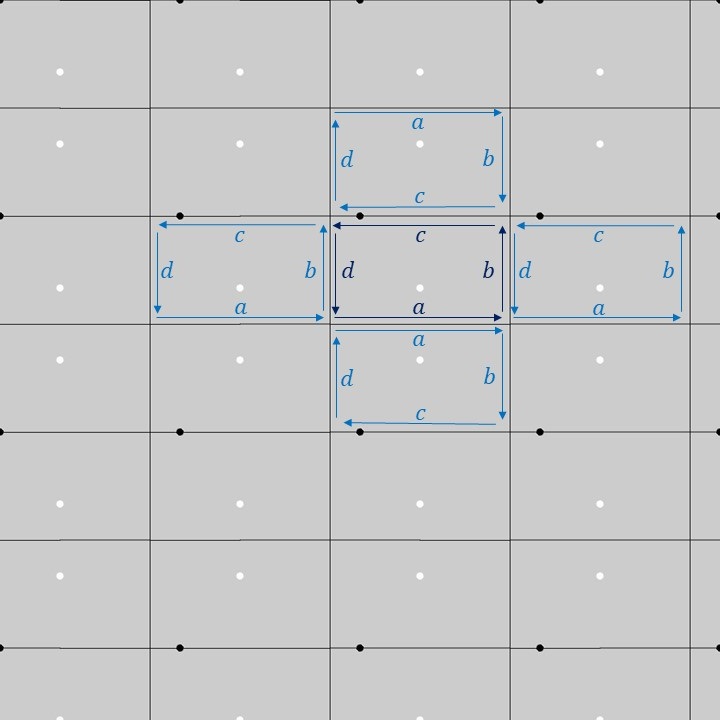
上図のように、1つの基本図形の長方形の各辺に\(a,b,c,d\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を長方格子上でPM群の対称性に合わせて移動させると、隣り合う長方形に対するラベルは薄い青色のラベルのようになります。隣り合う長方形同士の各辺の対応関係を見てみると、長方形の性質として、辺\(b\)と辺\(d\)の長さが等しく、互いに平行となっていることが分かります。これがPM群の基本図形に対する制約となっています。

なお、現段階ではこの制約は意味のあるものに見えませんが、今後「基本図形の変形」を考えていくときに重要になってきます。

PG群の基本図形の形状

PG群のボロノイ図

PG群の対称性をもつ母点に対してボロノイ図を作ってみます。

PG群のベースとなる長方格子の形状（黒点）に対して、1つの長方格子点から横隣りの格子点までの距離の3分の1、下隣りの格子点までの距離の3分の1の長さまで移動した位置にある点（白点）をとり、この点をPG群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

この結果から、PG群の基本図形は六角形になることが分かります。実際、下の図に示す通り、この図形は長方格子上での一方向のみ（赤い点線）の滑り鏡映変換（PG群の対称性）に対して不変になっています。

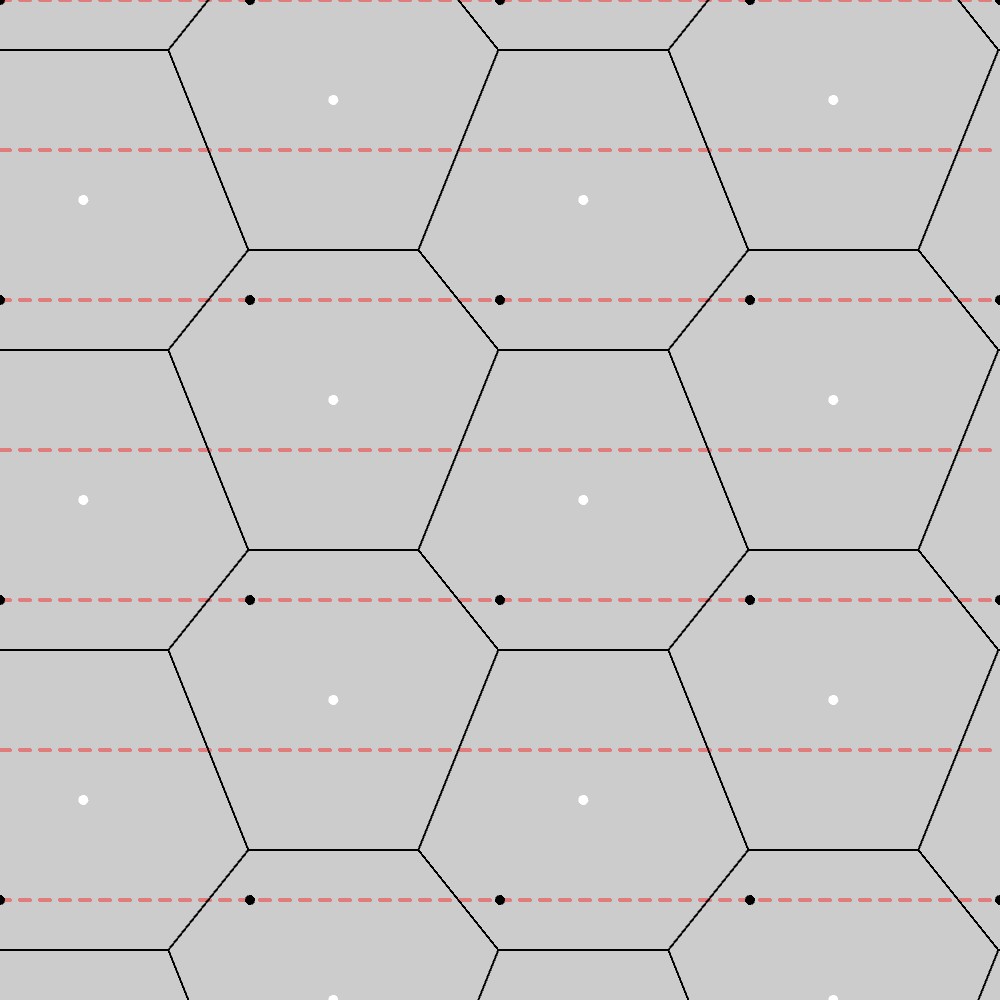
PG群の基本図形への制約

PG群によるボロノイ図から、PG群の基本図形への制約について考えてみます。

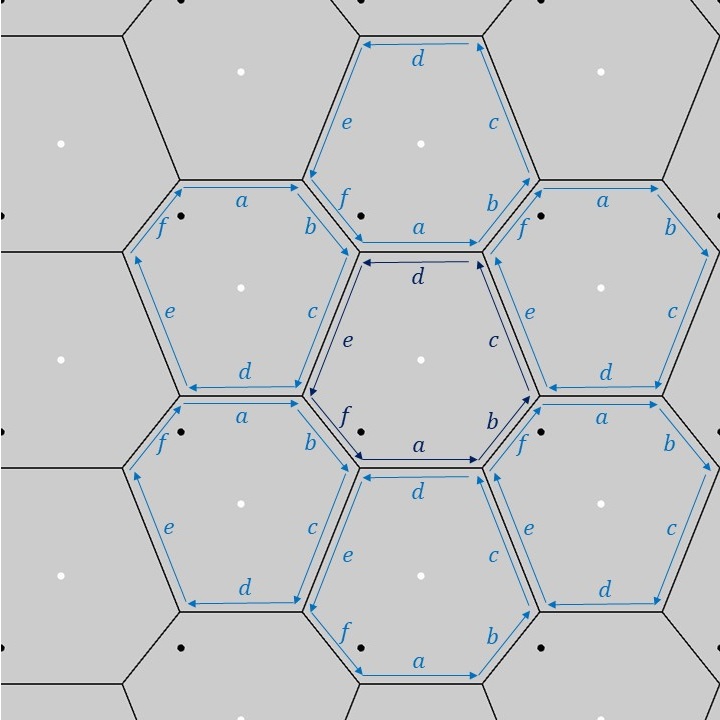
上図のように、1つの基本図形の六角形の各辺に\(a,b,c,d,e,f\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を長方格子上でPG群の対称性に合わせて移動させると、隣り合う六角形に対するラベルは薄い青色のラベルのようになります。隣り合う六角形同士の各辺の対応関係を見てみると、六角形の性質として、辺\(a\)と辺\(d\)の長さが等しく、互いに平行となっていて、辺\(b\)と辺\(f\)、辺\(c\)と辺\(e\)がそれぞれ長さが等しくなるように配置されることが分かります。これがPG群の基本図形に対する制約となっています。

なお、別記事「渦巻き図形」で直観的に選んだPG群の基本図形は長方形でした。これは六角形に対して辺\(b\)と辺\(f\)がそれぞれ縮んでその中点に収束した場合と考えることができます。

長方格子の縦横比を大きくした場合のPG群のボロノイ図

PG群の対称性をもつ母点に対するボロノイ図は長方格子の縦横比を大きくすると、別の形状をもつ基本図形が現れます。

長方格子の隣り合った点同士の距離で、短い方（今回は横方向）の距離を半分にします。長い方（今回は縦方向）の距離はそのままとします。

このとき、この長方格子の形状（黒点）に対して、1つの長方格子点から横隣りの格子点までの距離の2分の1、下隣りの格子点までの距離の3分の1の長さまで移動した位置にある点（白点）をとり、この点をPG群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

長方格子の縦横比を大きくした場合でもPG群の基本図形は六角形になることが分かり、また、下の図に示す通り、この図形は長方格子上での一方向のみ（赤い点線）の滑り鏡映変換（PG群の対称性）に対して不変になっています。

長方格子の縦横比を大きくした場合のPG群の基本図形への制約

長方格子の縦横比を大きくした場合のPG群によるボロノイ図から、新たに得られたPG群の基本図形への制約について考えてみます。

上図のように、1つの基本図形の六角形の各辺に\(a,b,c,d,e,f\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を長方格子上でPG群の対称性に合わせて移動させると、隣り合う六角形に対するラベルは薄い青色のラベルのようになります。隣り合う六角形同士の各辺の対応関係を見てみると、六角形の性質として、辺\(a\)と辺\(b\)、辺\(c\)と辺\(f\)、辺\(d\)と辺\(e\)がそれぞれ長さが等しくなるように配置されることが分かります。これがPG群の基本図形に対する制約となっています。

PMM群の基本図形の形状

PMM群のボロノイ図

PMM群の対称性をもつ母点に対してボロノイ図を作ってみます。

PMM群のベースとなる長方格子の形状（黒点）に対して、1つの長方格子点から横隣りの格子点までの距離の3分の1、下隣りの格子点までの距離の3分の1の長さまで移動した位置にある点（白点）をとり、この点をPMM群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

この結果から、PMM群の基本図形は長方形になることが分かります。実際、下の図に示す通り、この図形は長方格子上での縦横両方向（赤い線）の鏡映変換および赤点を中心とした180°回転（PMM群の対称性）に対して不変になっています。

PMM群の基本図形への制約

PMM群によるボロノイ図から、PMM群の基本図形への制約について考えてみます。

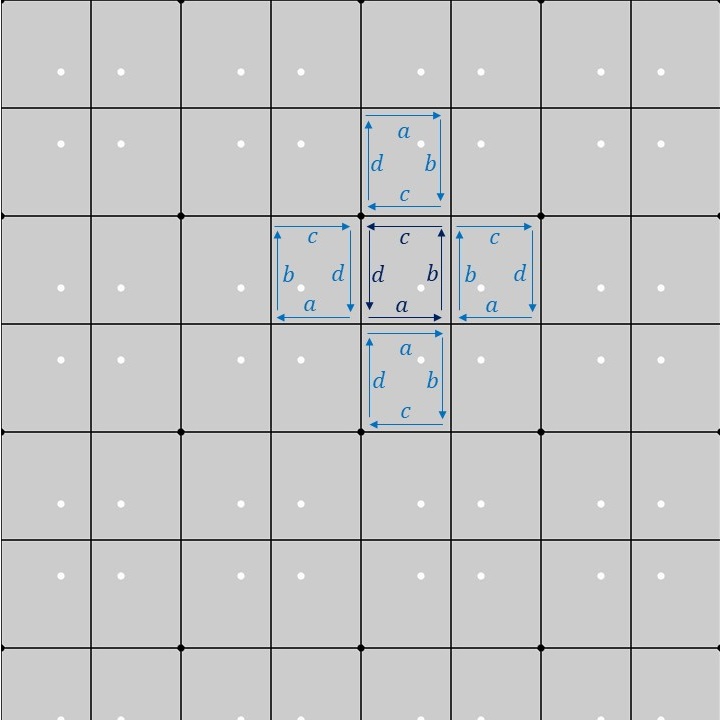
上図のように、1つの基本図形の長方形の各辺に\(a,b,c,d\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を長方格子上でPMM群の対称性に合わせて移動させると、隣り合う長方形に対するラベルは薄い青色のラベルのようになります。隣り合う長方形同士の各辺の対応関係を見てみると、PMM群の基本図形については長方形になるという以外、特に制約はないようです。

PMG群の基本図形の形状

PMG群のボロノイ図

PMG群の対称性をもつ母点に対してボロノイ図を作ってみます。ただし、PMG群の場合、2つのケースが考えられます。

ケース１：五角形

PMG群のベースとなる長方格子の形状（黒点）に対して、1つの長方格子点から横隣りの格子点までの距離の3分の1、下隣りの格子点までの距離の3分の1の長さまで移動した位置にある点（白点）をとり、この点をPMG群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

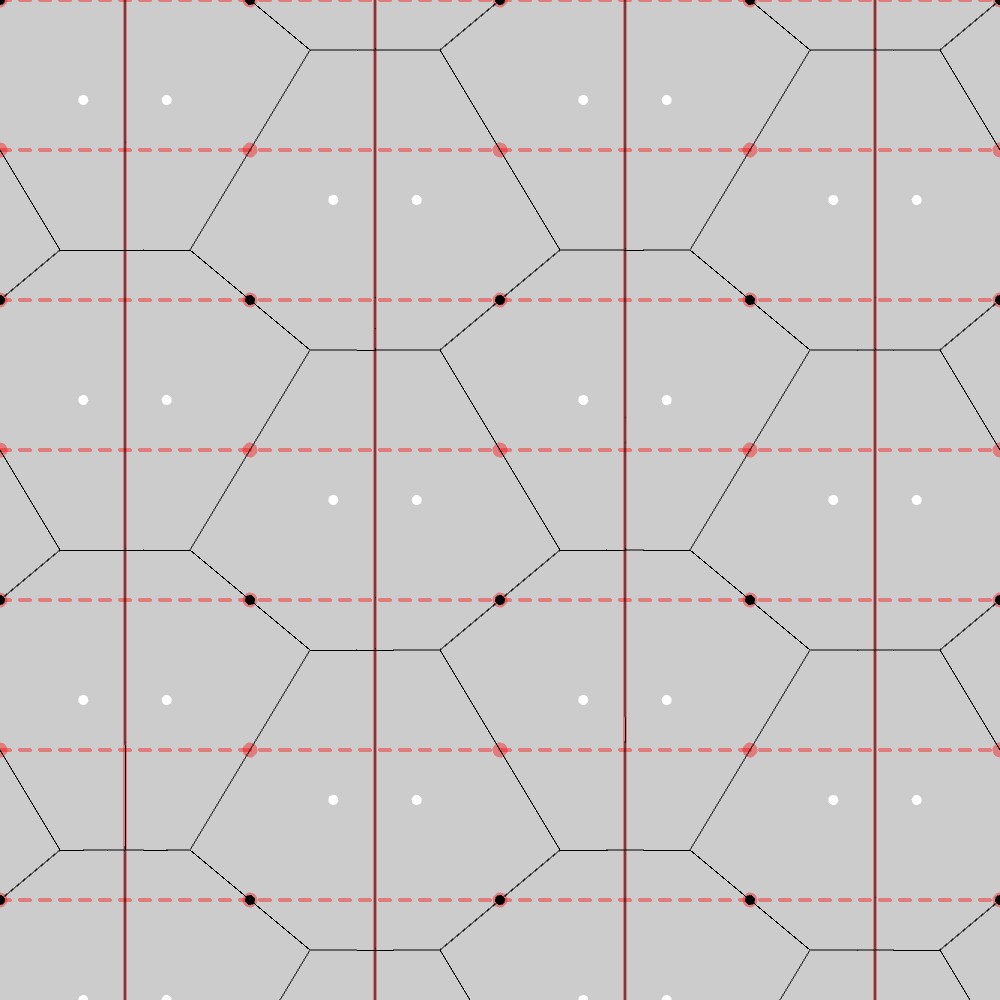
この結果から、PMG群の基本図形の一つは五角形になることが分かります。実際、下図に示す通り、この図形は長方格子上での横方向の滑り鏡映変換（赤い点線）、縦方向の鏡映変換（赤い線）および赤点を中心とした180°回転（PMG群の対称性）に対して不変になっています。

ケース２：台形

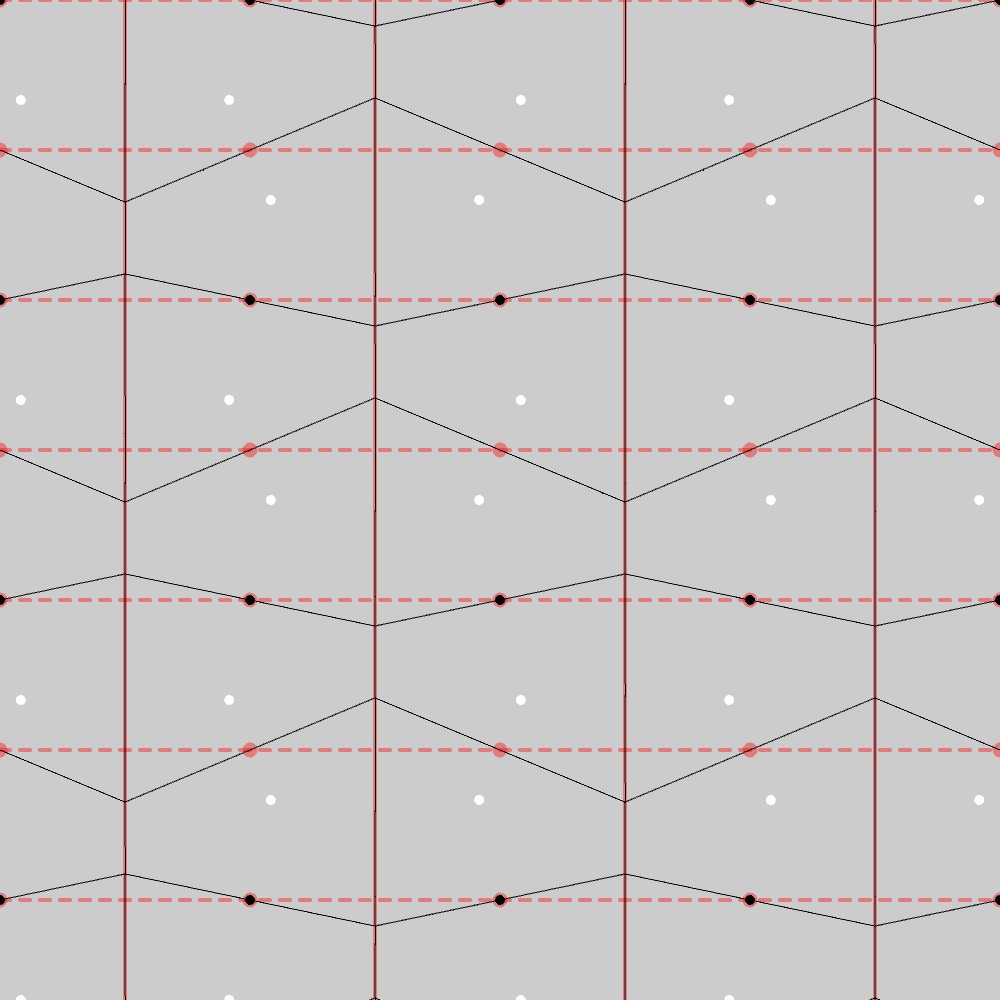
PMG群のベースとなる長方格子の形状（黒点）に対して、1つの長方格子点から横隣りの格子点までの距離の12分の1、下隣りの格子点までの距離の3分の1の長さまで移動した位置にある点（白点）をとり、この点をPMG群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

この結果から、PMG群の基本図形のもう一つは台形になることが分かります。実際、下図に示す通り、この図形は長方格子上でPMG群の対称性を満たしています。

PMG群の基本図形への制約

PMG群によるボロノイ図から、PMG群の基本図形への制約について考えてみます。

ケース１：五角形

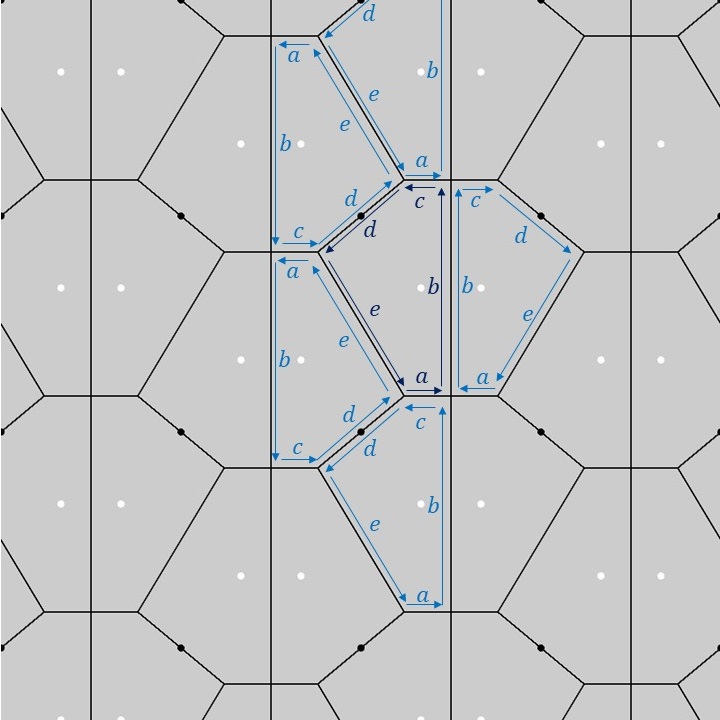
上図のように、1つの基本図形の五角形の各辺に\(a,b,c,d,e\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を長方格子上でPMG群の対称性に合わせて移動させると、隣り合う五角形に対するラベルは薄い青色のラベルのようになります。隣り合う五角形同士の各辺の対応関係を見てみると、五角形の性質として、辺\(a\)と辺\(c\)の長さが等しく、互いに平行となるように配置されることが分かります。これがPMG群の基本図形に対する制約となっています。

ケース２：台形

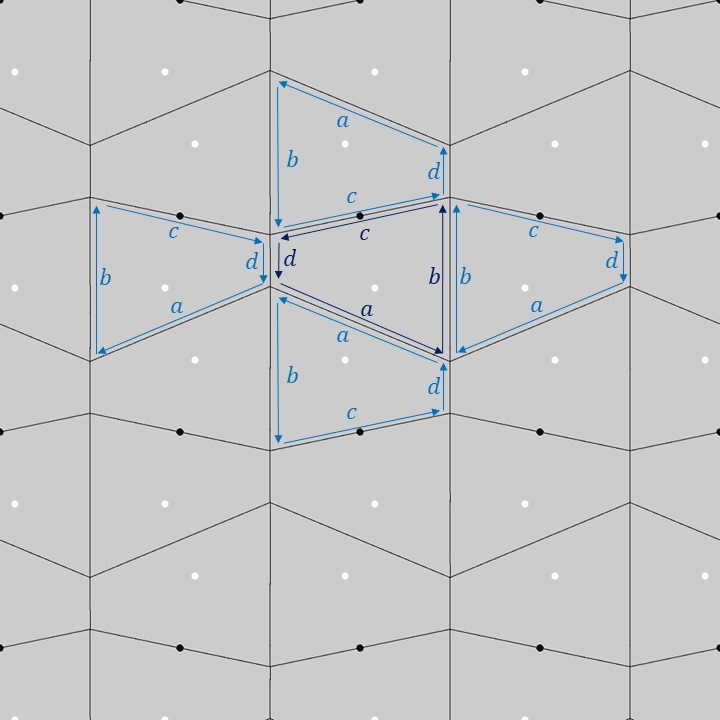
上図のように、もう1つの基本図形の台形の各辺に\(a,b,c,d\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を菱形格子上でPMG群の対称性に合わせて移動させると、隣り合う台形に対するラベルは薄い青色のラベルのようになります。隣り合う台形同士の各辺の対応関係を見てみると、PMG群の基本図形である台形に対しては、台形となるという以上の制約はないようです。

PGG群の基本図形の形状

PGG群のボロノイ図

PGG群の対称性をもつ母点に対してボロノイ図を作ってみます。

PGG群のベースとなる長方格子の形状（黒点）に対して、1つの長方格子点から横隣りの格子点までの距離の3分の1、下隣りの格子点までの距離の3分の1の長さまで移動した位置にある点（白点）をとり、この点をPGG群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

この結果から、PGG群の基本図形は六角形になることが分かります。実際、下図に示す通り、この図形は長方格子上での縦横方向の滑り鏡映変換（赤い点線）および赤点を中心とした180°回転（PGG群の対称性）に対して不変になっています。

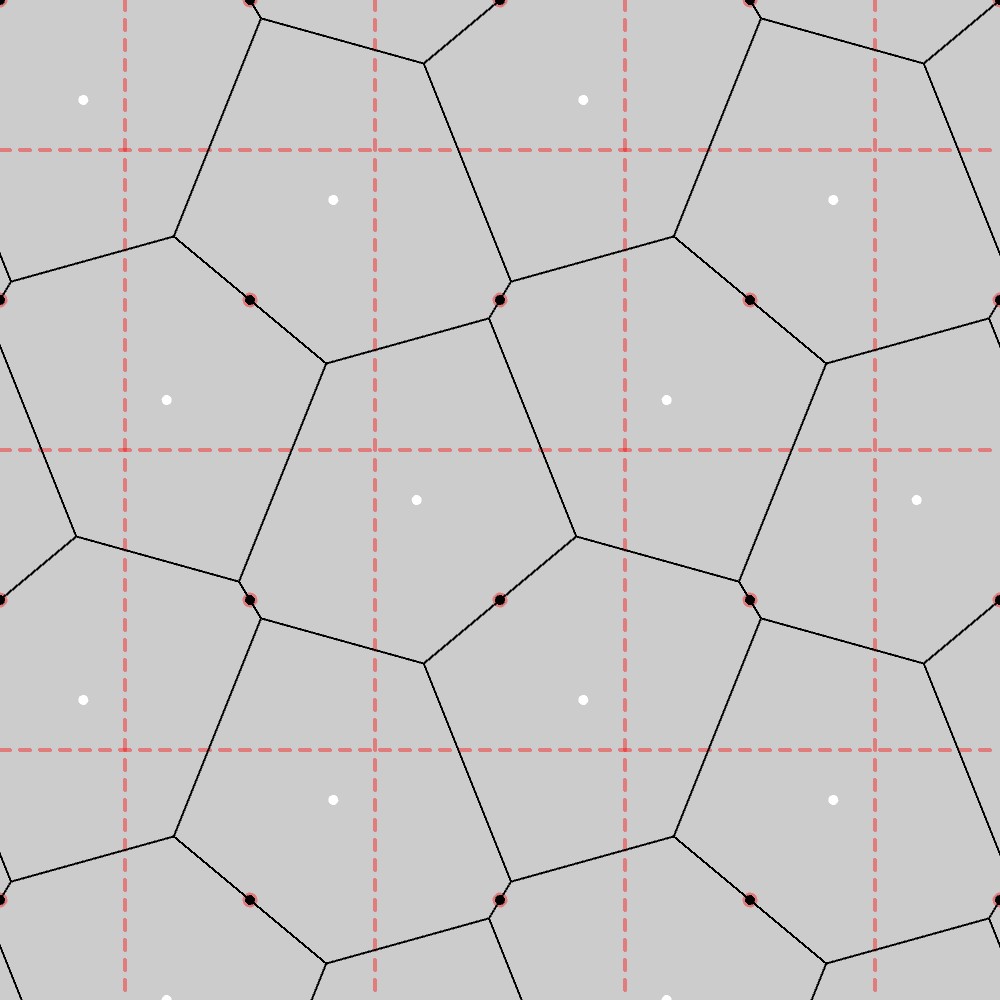
PGG群の基本図形への制約

PGG群によるボロノイ図から、PGG群の基本図形への制約について考えてみます。

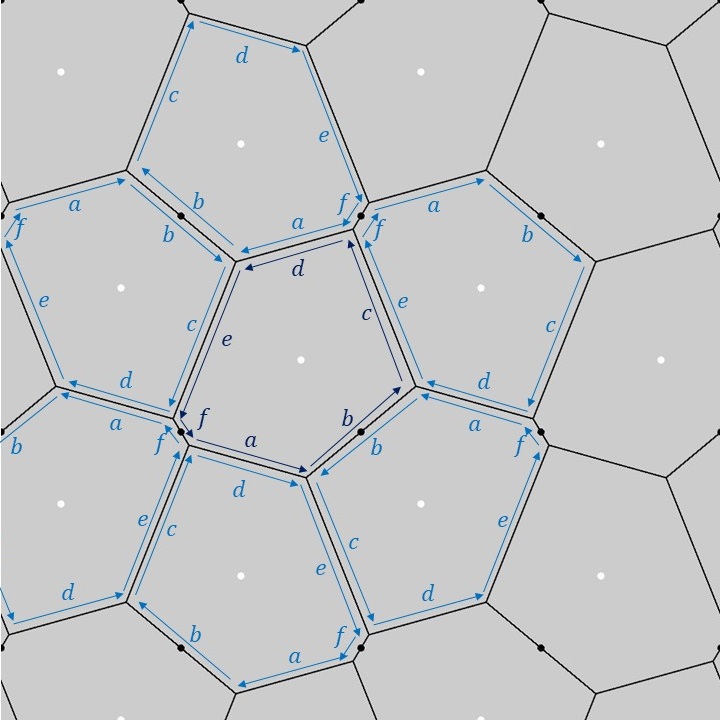
上図のように、1つの基本図形の六角形の各辺に\(a,b,c,d,e,f\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を長方格子上でPGG群の対称性に合わせて移動させると、隣り合う六角形に対するラベルは薄い青色のラベルのようになります。隣り合う六角形同士の各辺の対応関係を見てみると、六角形の性質として、辺\(a\)と辺\(d\)、辺\(c\)と辺\(e\)のそれぞれ長さが等しくなるように配置されることが分かります。これがPGG群の基本図形に対する制約となっています。

なお、別記事「渦巻き図形」で直観的に選んだPGG群の基本図形は長方形でした。これは六角形に対して辺\(b\)と辺\(f\)がそれぞれ縮んでその中点に収束した場合と考えることができます。

長方格子の縦横比を大きくした場合のPGG群のボロノイ図

PGG群の対称性をもつ母点に対するボロノイ図は長方格子の縦横比を大きくすると、別の形状をもつ基本図形が現れます。

長方格子の隣り合った点同士の距離で、短い方（今回は横方向）の距離を半分にします。長い方（今回は縦方向）の距離はそのままとします。

このとき、この長方格子の形状（黒点）に対して、1つの長方格子点から横隣りの格子点までの距離の3分の1、下隣りの格子点までの距離の3分の1の長さまで移動した位置にある点（白点）をとり、この点をPGG群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

長方格子の縦横比を大きくした場合でもPGG群の基本図形は六角形になることが分かり、また、下の図に示す通り、この図形は長方格子上での縦横方向の滑り鏡映変換（赤い点線）および赤点を中心とした180°回転（PGG群の対称性）に対して不変になっています。

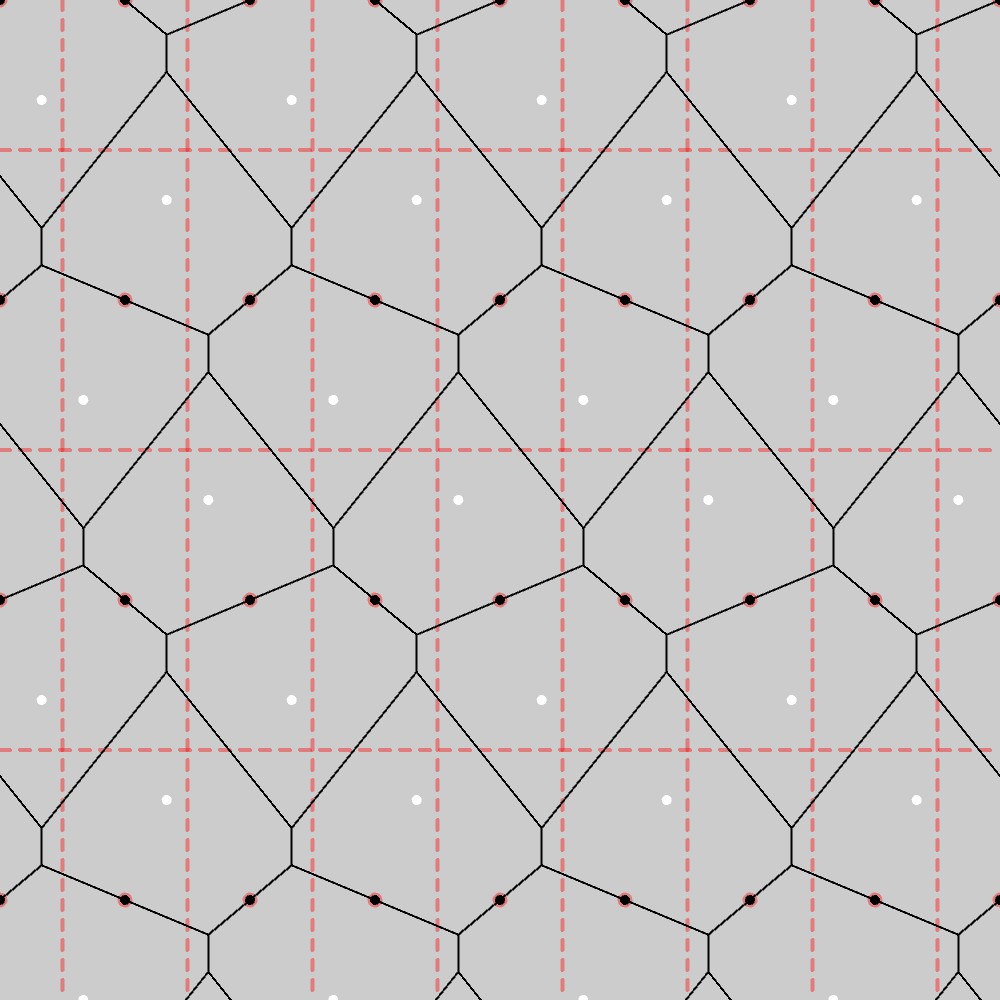
長方格子の縦横比を大きくした場合のPGG群の基本図形への制約

長方格子の縦横比を大きくした場合のPGG群によるボロノイ図から、新たに得られたPGG群の基本図形への制約について考えてみます。

上図のように、1つの基本図形の六角形の各辺に\(a,b,c,d,e,f\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を長方格子上でPGG群の対称性に合わせて移動させると、隣り合う六角形に対するラベルは薄い青色のラベルのようになります。隣り合う六角形同士の各辺の対応関係を見てみると、六角形の性質として、辺\(c\)と辺\(f\)、辺\(d\)と辺\(e\)がそれぞれ長さが等しくなるように配置されることが分かります。これがPGG群の基本図形に対する制約となっています。

CM群の基本図形の形状

CM群のボロノイ図

CM群の対称性をもつ母点に対してボロノイ図を作ってみます。ただし、CM群の場合、2つのケースが考えられます。

ケース１：五角形

CM群のベースとなる菱形格子の形状（黒点）に対して、1つの菱形格子点から横隣りの格子点までの距離の3分の1、右斜め下の格子点までの距離の3分の1の長さまで移動した位置にある点（白点）をとり、この点をCM群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

この結果から、CM群の基本図形の一つは五角形になることが分かります。実際、下図に示す通り、この図形は菱形格子上での横方向の鏡映変換（赤い線）および滑り鏡映変換（赤い点線）（合わせてCM群の対称性）に対して不変になっています。

ケース２：台形

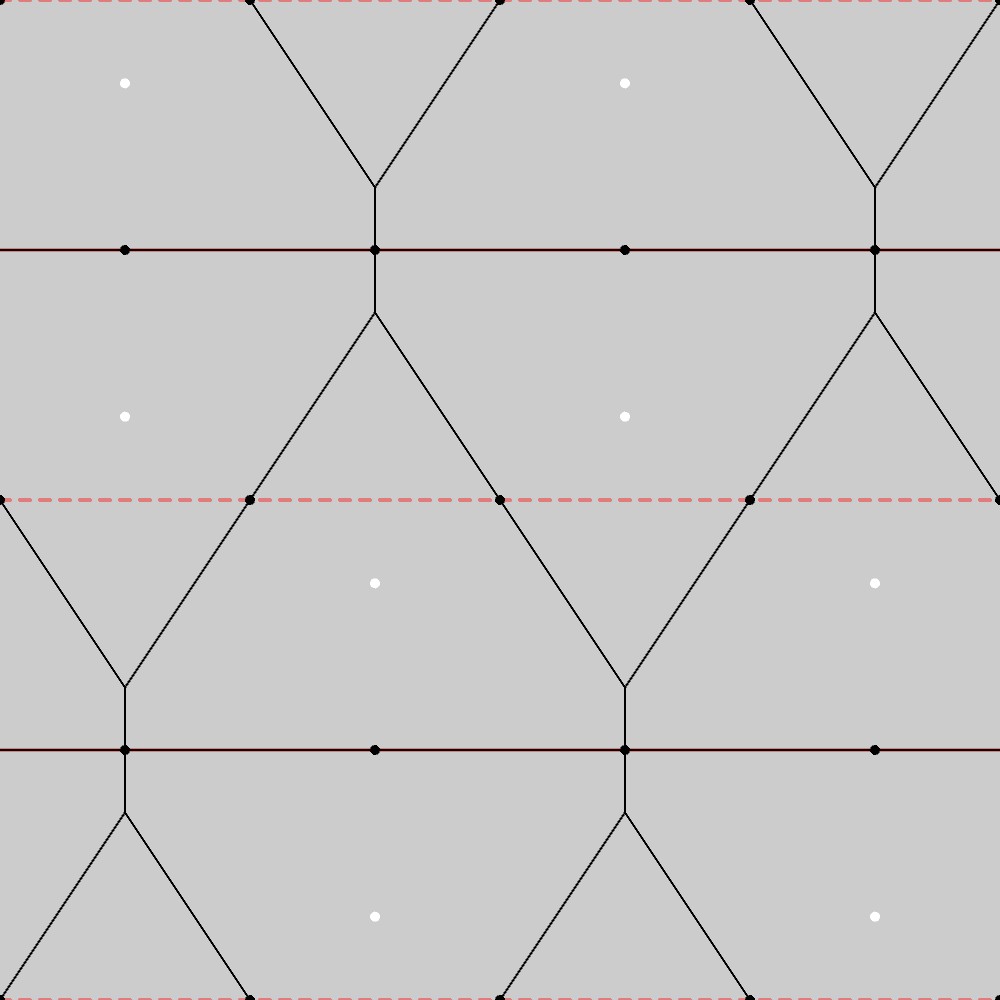
CM群のベースとなる菱形格子の形状（黒点）に対して、1つの菱形格子点から横隣りの格子点までの距離の5分の2、右斜め下の格子点までの距離の5分の1の長さまで移動した位置にある点（白点）をとり、この点をCM群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

この結果から、CM群の基本図形のもう一つは台形になることが分かります。実際、下図に示す通り、この図形は菱形格子上でのCM群の対称性を満たしています。

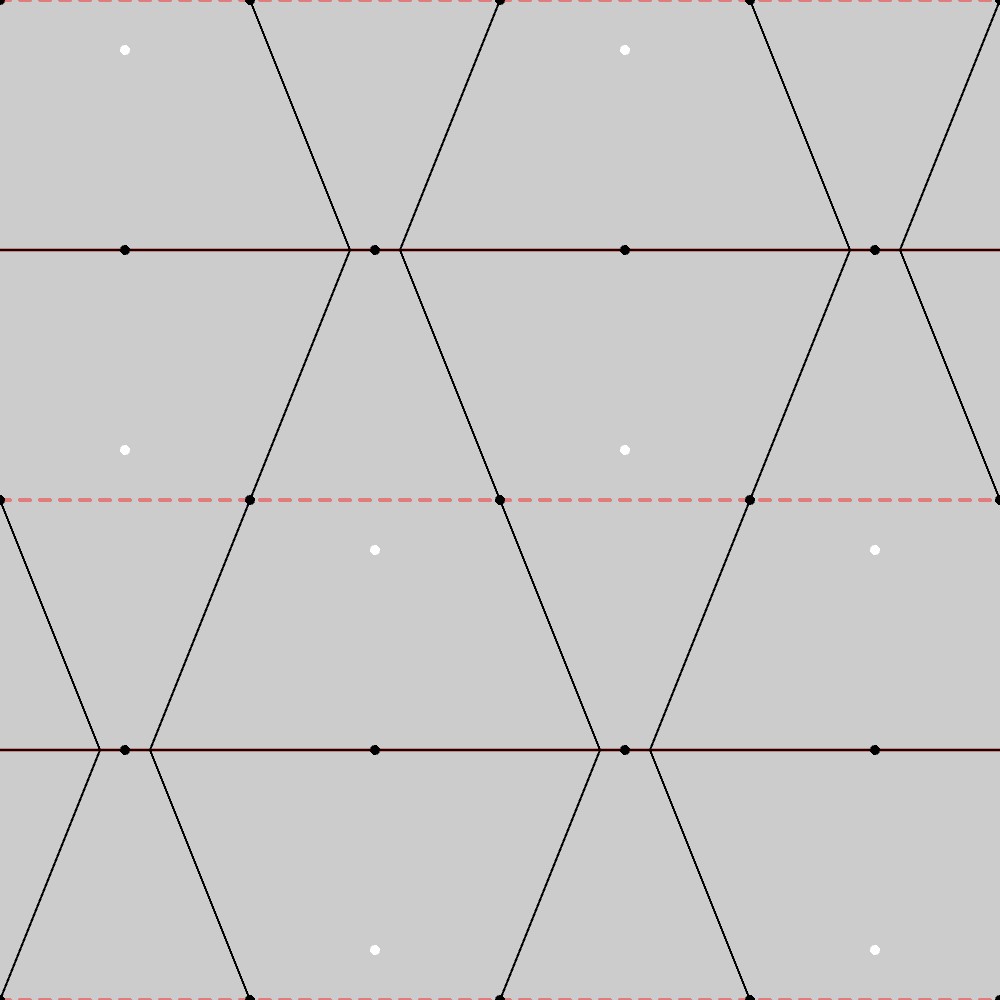
CM群の基本図形への制約

CM群によるボロノイ図から、CM群の基本図形への制約について考えてみます。

ケース１：五角形

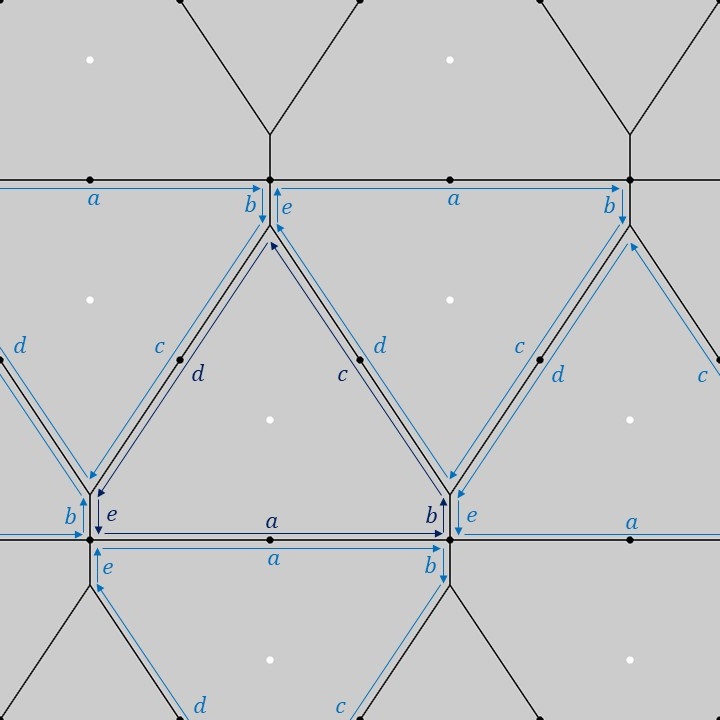
上図のように、1つの基本図形の五角形の各辺に\(a,b,c,d,e\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を菱形格子上でCM群の対称性に合わせて移動させると、隣り合う五角形に対するラベルは薄い青色のラベルのようになります。隣り合う五角形同士の各辺の対応関係を見てみると、五角形の性質として、辺\(b\)と辺\(e\)の長さが等しくて平行、辺\(c\)と辺\(d\)の長さが等しくなるように配置されることが分かります。これがCM群の基本図形である五角形に対する制約となっています。

ケース２：台形

上図のように、もう1つの基本図形の台形の各辺に\(a,b,c,d\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を菱形格子上でCM群の対称性に合わせて移動させると、隣り合う台形に対するラベルは薄い青色のラベルのようになります。隣り合う台形同士の各辺の対応関係を見てみると、台形の性質として、辺\(b\)と辺\(d\)の長さが等しくなるように配置されることが分かります。これがCM群の基本図形である台形に対する制約となっています。

なお、別記事「渦巻き図形」で直観的に選んだCM群の基本図形は長方形でした。これは台形に対して辺\(a\)と辺\(c\)の長さが同じになった場合と考えることができます。

CMM群の基本図形の形状

CMM群のボロノイ図

CMM群の対称性をもつ母点に対してボロノイ図を作ってみます。

CMM群のベースとなる菱形格子の形状（黒点）に対して、1つの菱形格子点から横隣りの格子点までの距離の5分の1、右斜め下の格子点までの距離の4分の1の長さまで移動した位置にある点（白点）をとり、この点をCMM群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

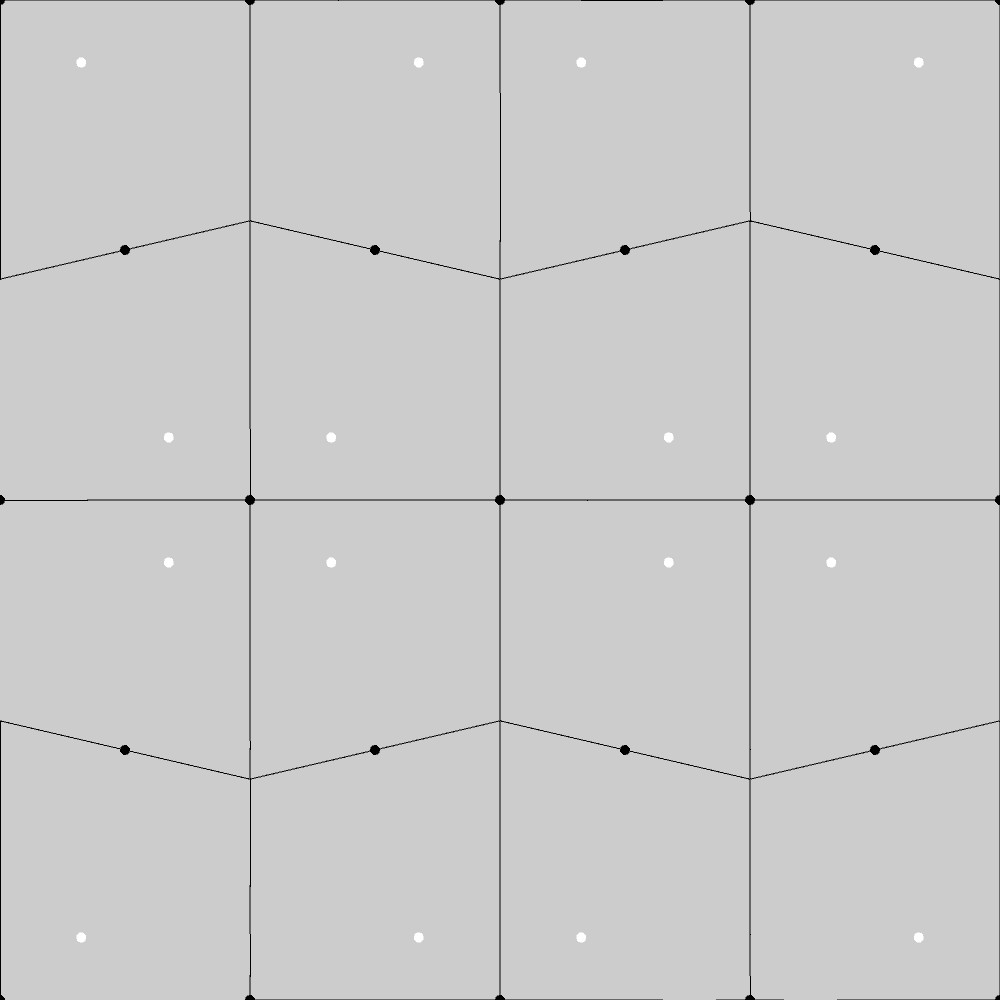
この結果から、CMM群の基本図形は台形になることが分かります。実際、下図に示す通り、この図形は菱形格子上での縦横方向の鏡映変換（赤い線）と滑り鏡映変換（赤い点線）および赤点を中心とした180°回転（CMM群の対称性）に対して不変になっています。

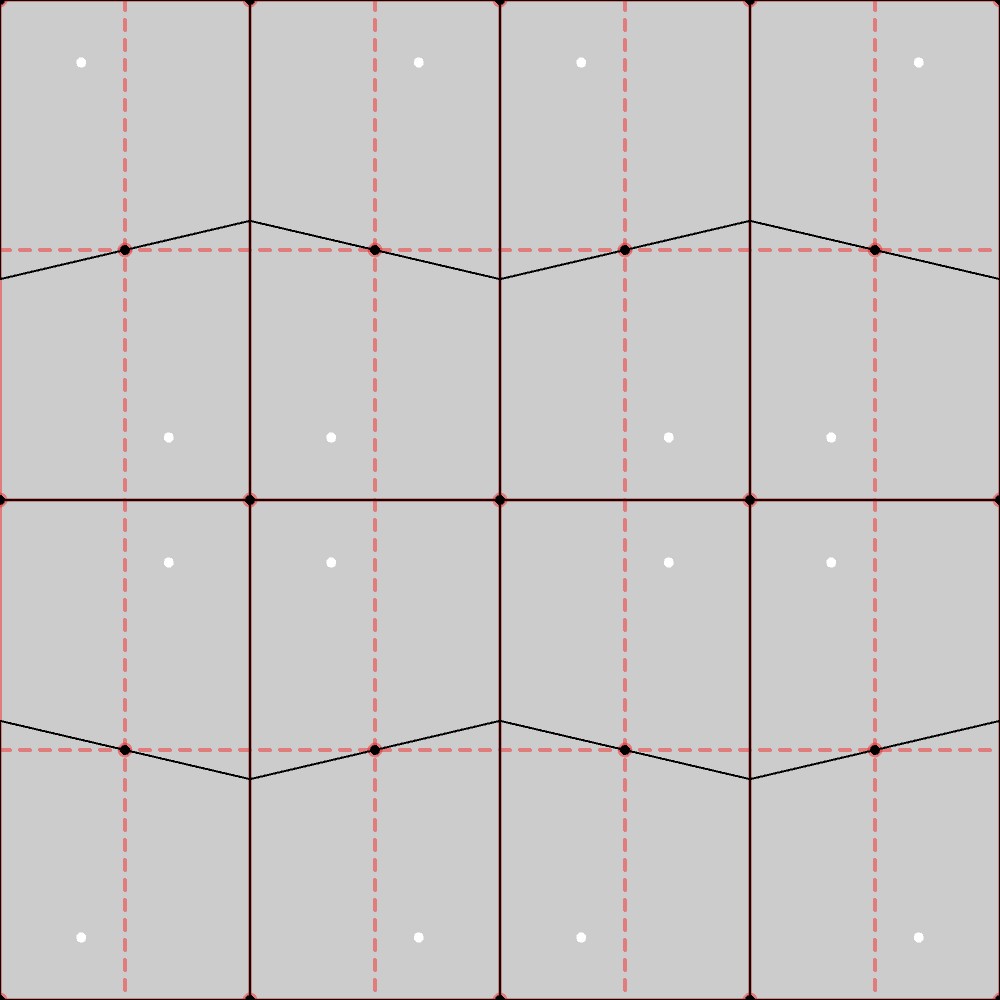
CMM群の基本図形への制約

CMM群によるボロノイ図から、CMM群の基本図形への制約について考えてみます。

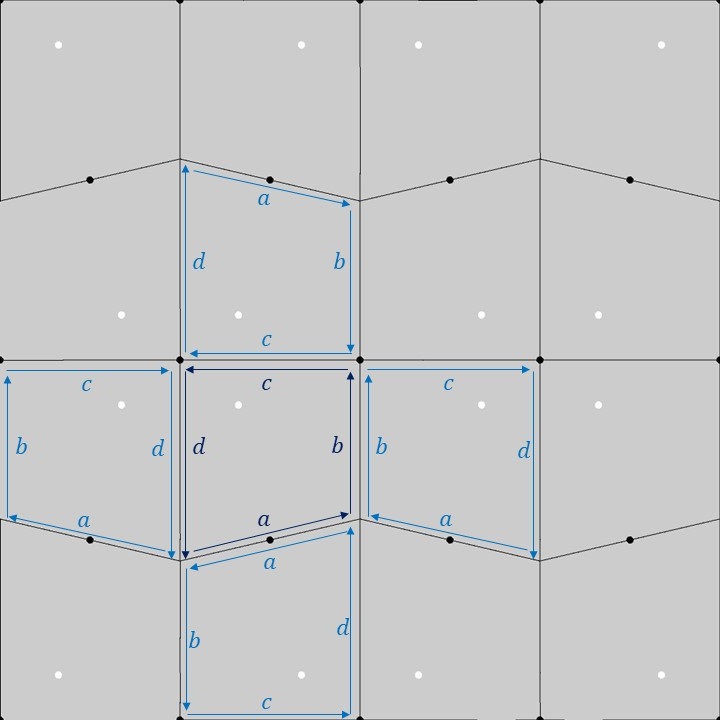
上図のように、１つの基本図形の台形の各辺に\(a,b,c,d\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を菱形格子上でCMM群の対称性に合わせて移動させると、隣り合う台形に対するラベルは薄い青色のラベルのようになります。隣り合う台形同士の各辺の対応関係を見てみると、台形の性質として、辺\(b\)と辺\(c\)のなす角、辺\(c\)と辺\(d\)のなす角がそれぞれ90°になるように配置されることが分かります。これがCMM群の基本図形に対する制約となっています。

なお、別記事「渦巻き図形」で直観的に選んだCMM群の基本図形は長方形でした。これは台形に対して辺\(b\)と辺\(d\)の長さが同じになった場合と考えることができます。

P4群の基本図形の形状

P4群のボロノイ図

P4群の対称性をもつ母点に対してボロノイ図を作ってみます。

P4群のベースとなる正方格子の形状（黒点）に対して、1つの正方格子点から横隣りの格子点までの距離の3分の1、下隣りの格子点までの距離の4分の1の長さまで移動した位置にある点（白点）をとり、この点をP4群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

この結果から、P4群の基本図形は五角形になることが分かります。実際、下図に示す通り、この図形は正方格子上で赤四角点を中心とした90°回転および赤点を中心とした180°回転（P4群の対称性）に対して不変になっています。

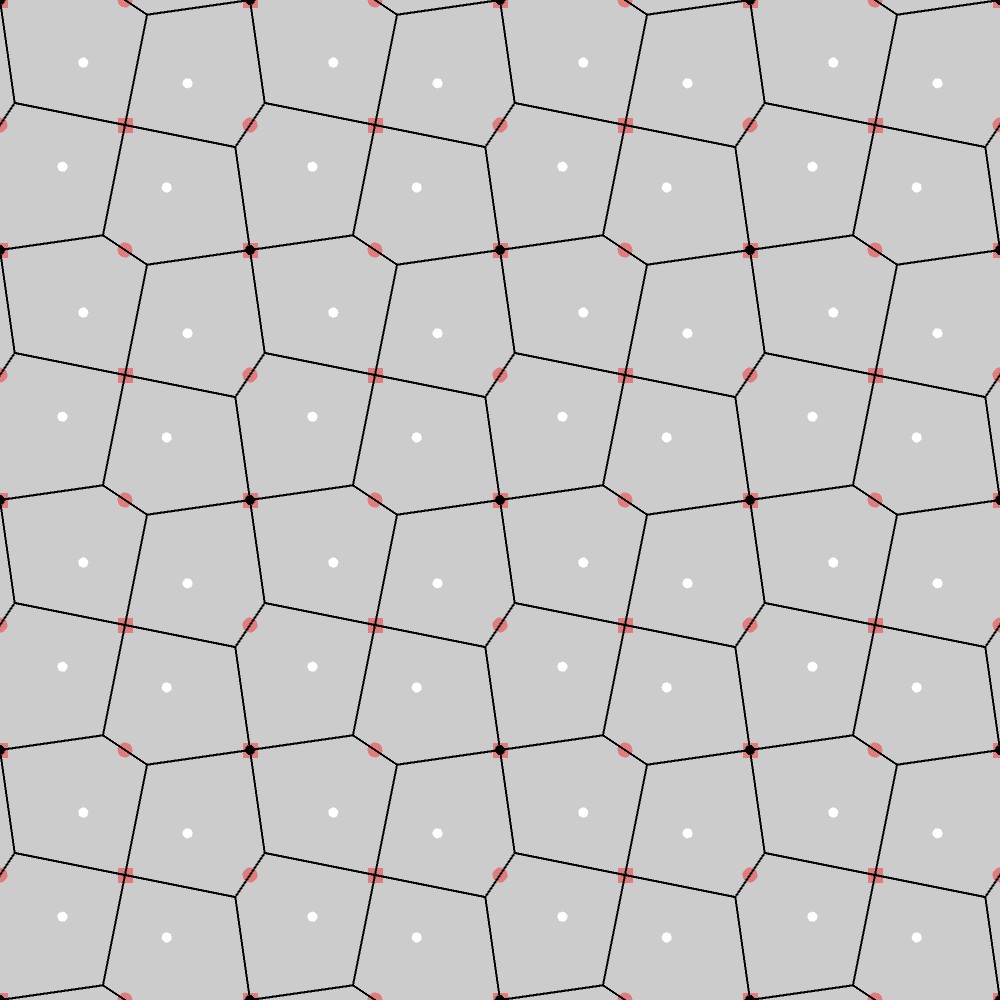
P4群の基本図形への制約

P4群によるボロノイ図から、P4群の基本図形への制約について考えてみます。

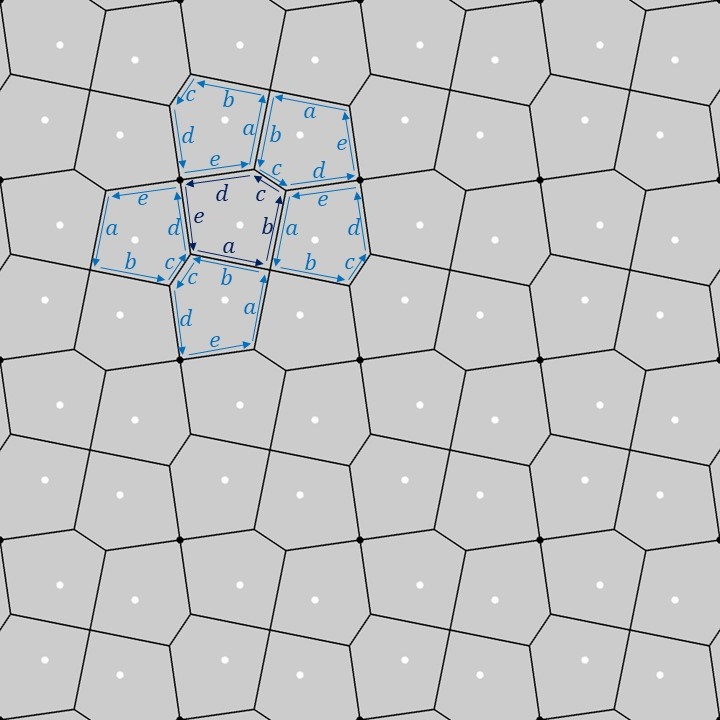
上図のように、１つの基本図形の五角形の各辺に\(a,b,c,d,e\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を正方格子上でP4群の対称性に合わせて移動させると、隣り合う五角形に対するラベルは薄い青色のラベルのようになります。隣り合う五角形同士の各辺の対応関係を見てみると、五角形の性質として、辺\(a\)と辺\(b\)、辺\(d\)と辺\(e\)のそれぞれの長さが等しく、なす角が90°になるように配置されることが分かります。これがP4群の基本図形に対する制約となっています。

なお、別記事「渦巻き図形」で直観的に選んだP4群の基本図形は正方形でした。これは五角形に対して辺\(c\)が縮んでその中点に収束した場合と考えることができます。

P4M群の基本図形の形状

P4M群のボロノイ図

P4M群の対称性をもつ母点に対してボロノイ図を作ってみます。

P4M群のベースとなる正方格子の形状（黒点）に対して、1つの正方格子点から横隣りの格子点までの距離の2分の1、下隣りの格子点までの距離の4分の1の長さまで移動した位置にある点（白点）をとり、この点をP4M群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

この結果から、P4M群の基本図形は直角二等辺三角形になることが分かります。実際、下図に示す通り、この図形は正方格子上で横縦斜め方向の鏡映変換（赤い線）と滑り鏡映変換（赤い点線）、赤四角点を中心とした90°回転および赤点を中心とした180°回転（P4M群の対称性）に対して不変になっています。

P4M群の基本図形への制約

P4M群によるボロノイ図から、P4M群の基本図形への制約について考えてみます。

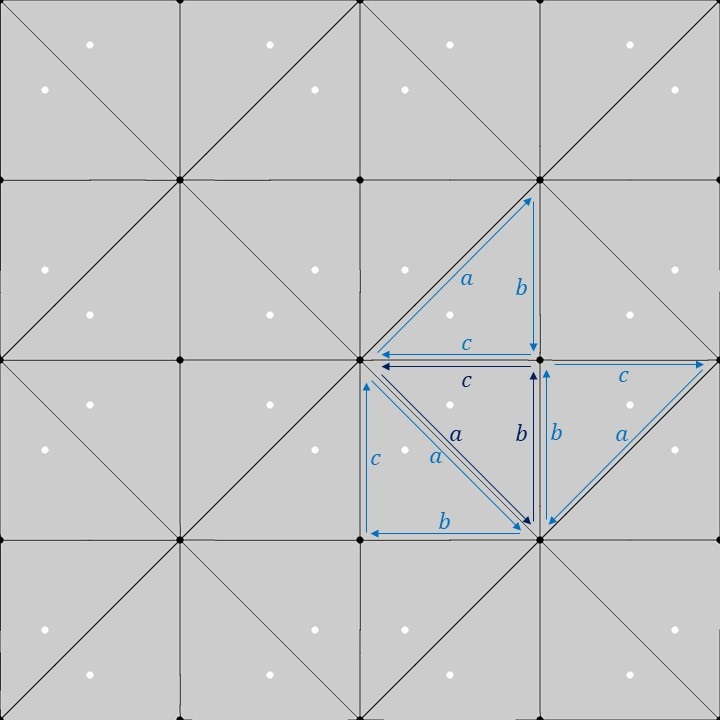
上図のように、１つの基本図形の直角二等辺三角形の各辺に\(a,b,c\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を正方格子上でP4M群の対称性に合わせて移動させると、隣り合う直角二等辺三角形に対するラベルは薄い青色のラベルのようになります。隣り合う直角二等辺三角形同士の各辺の対応関係を見てみると、P4M群の基本図形については直角二等辺三角形になるという以外、特に制約はないようです。

P4G群の基本図形の形状

P4G群のボロノイ図

P4G群の対称性をもつ母点に対してボロノイ図を作ってみます。

P4M群のベースとなる正方格子の形状（黒点）に対して、1つの正方格子点から横隣りの格子点までの距離の3分の1、下隣りの格子点までの距離の4分の1の長さまで移動した位置にある点（白点）をとり、この点をP4G群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

この結果から、P4G群の基本図形は四角形になることが分かります。実際、下図に示す通り、この図形は正方格子上で横縦斜め方向の鏡映変換（赤い線）と滑り鏡映変換（赤い点線）、赤四角点を中心とした90°回転および赤点を中心とした180°回転（P4G群の対称性）に対して不変になっています。

P4G群の基本図形への制約

P4G群によるボロノイ図から、P4G群の基本図形への制約について考えてみます。

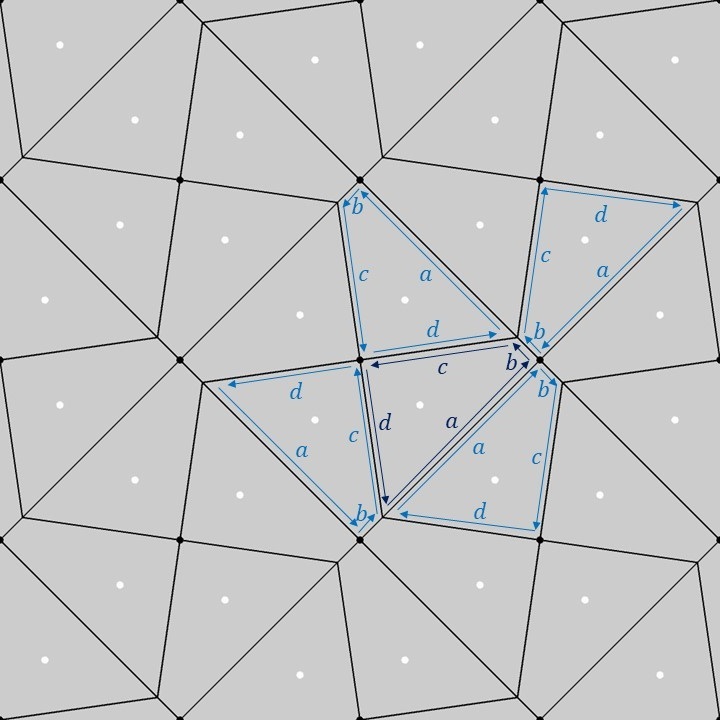
上図のように、１つの基本図形の四角形の各辺に\(a,b,c,d\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を正方格子上でP4G群の対称性に合わせて移動させると、隣り合う四角形に対するラベルは薄い青色のラベルのようになります。隣り合う四角形同士の各辺の対応関係を見てみると、四角形の性質として、辺\(a\)と辺\(b\)のなす角が90°、辺\(c\)と辺\(d\)の長さが等しく、なす角が90°になるように配置されることが分かります。これがP4G群の基本図形に対する制約となっています。

P3群の基本図形の形状

P3群のボロノイ図

P3群の対称性をもつ母点に対してボロノイ図を作ってみます。

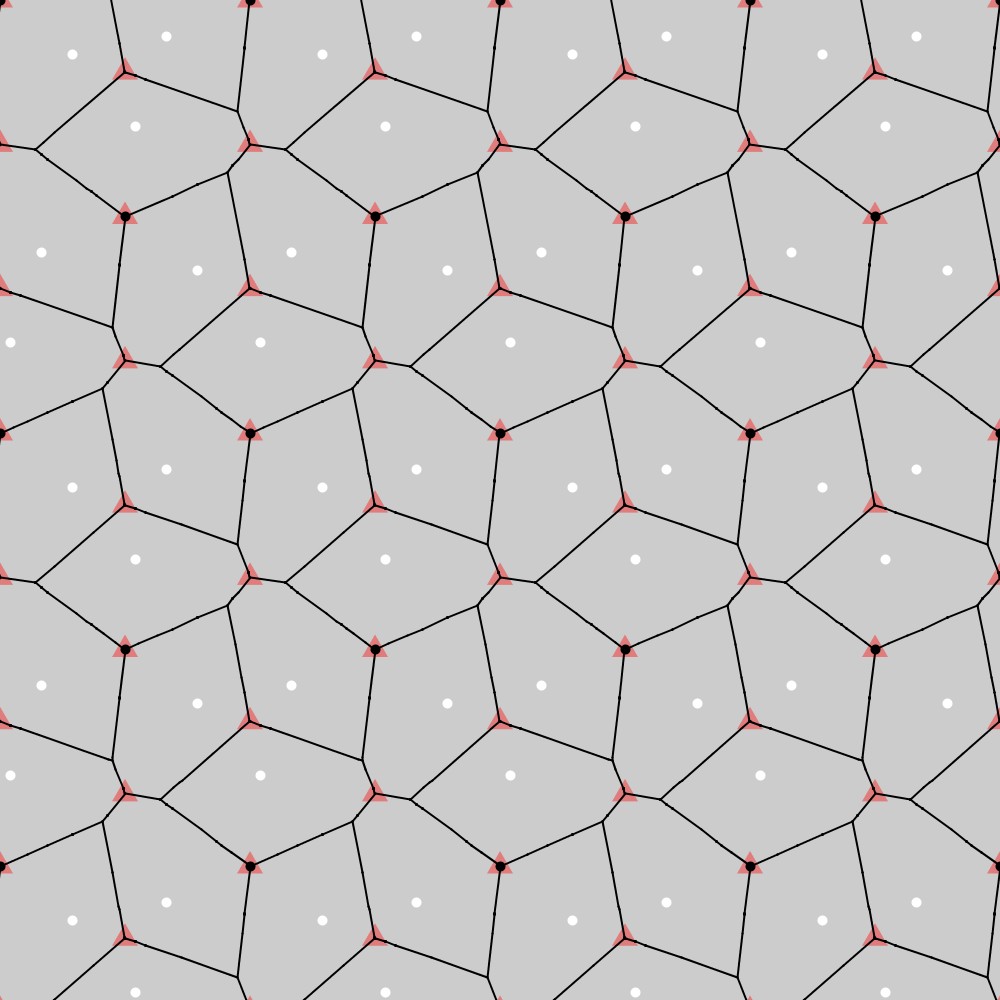
P3群のベースとなる三角格子の形状（黒点）に対して、1つの三角格子点から横隣りの格子点までの距離の6分の1、右斜め下の格子点までの距離の4分の1の長さまで移動した位置にある点（白点）をとり、この点をP3群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

この結果から、P3群の基本図形は六角形になることが分かります。実際、下図に示す通り、この図形は三角格子上で赤三角点を中心とした120°回転（P3群の対称性）に対して不変になっています。

P3群の基本図形への制約

P3群によるボロノイ図から、P3群の基本図形への制約について考えてみます。

上図のように、１つの基本図形の六角形の各辺に\(a,b,c,d,e,f\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を三角格子上でP3群の対称性に合わせて移動させると、隣り合う六角形に対するラベルは薄い青色のラベルのようになります。隣り合う六角形同士の各辺の対応関係を見てみると、六角形の性質として、辺\(a\)と辺\(b\)、辺\(c\)と辺\(d\)、辺\(e\)と辺\(f\)のそれぞれ長さが等しく、なす角が120°になるように配置されることが分かります。これがP3群の基本図形に対する制約となっています。

P3M1群の基本図形の形状

P3M1群のボロノイ図

P3M1群の対称性をもつ母点に対してボロノイ図を作ってみます。

P3M1群のベースとなる三角格子の形状（黒点）に対して、1つの三角格子点から横隣りの格子点までの距離の3分の1、右斜め下の格子点までの距離の4分の1の長さまで移動した位置にある点（白点）をとり、この点をP3M1群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

この結果から、P3M1群の基本図形は正三角形になることが分かります。実際、下図に示す通り、この図形は三角格子上で縦斜め方向の鏡映変換（赤い線）と滑り鏡映変換（赤い点線）、および赤三角点を中心とした120°回転（P3M1群の対称性）に対して不変になっています。

P3M1群の基本図形への制約

P3M1群によるボロノイ図から、P3M1群の基本図形への制約について考えてみます。

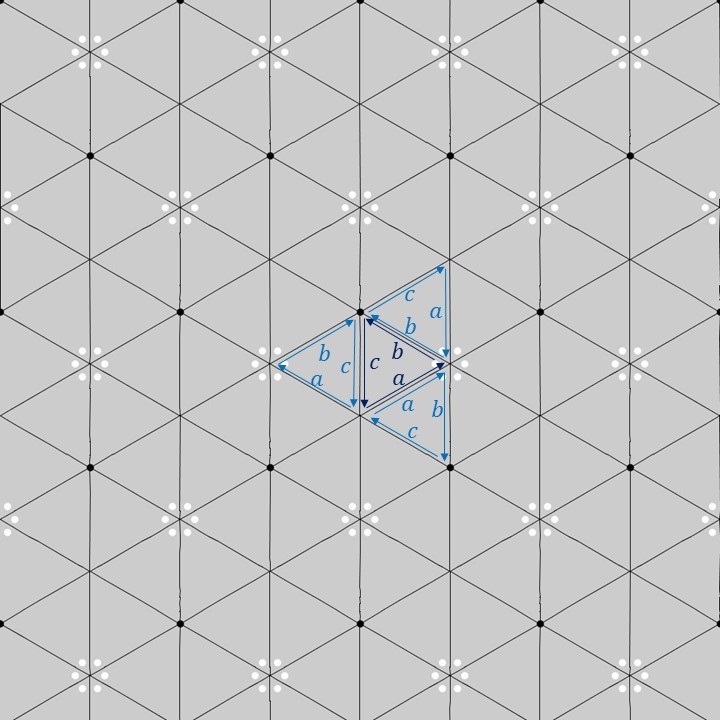
上図のように、１つの基本図形の正三角形の各辺に\(a,b,c\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を三角格子上でP3M1群の対称性に合わせて移動させると、隣り合う正三角形に対するラベルは薄い青色のラベルのようになります。隣り合う正三角形同士の各辺の対応関係を見てみると、P3M1群の基本図形については正三角形になるという以外、特に制約はないようです。

P31M群の基本図形の形状

P31M群のボロノイ図

P31M群の対称性をもつ母点に対してボロノイ図を作ってみます。

P31M群のベースとなる三角格子の形状（黒点）に対して、1つの三角格子点から横隣りの格子点までの距離の10分の1、右斜め下の格子点までの距離の4分の1の長さまで移動した位置にある点（白点）をとり、この点をP31M群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

この結果から、P31M群の基本図形は四角形になることが分かります。実際、下図に示す通り、この図形は三角格子上で横斜め方向の鏡映変換（赤い線）と滑り鏡映変換（赤い点線）、および赤三角点を中心とした120°回転（P31M群の対称性）に対して不変になっています。

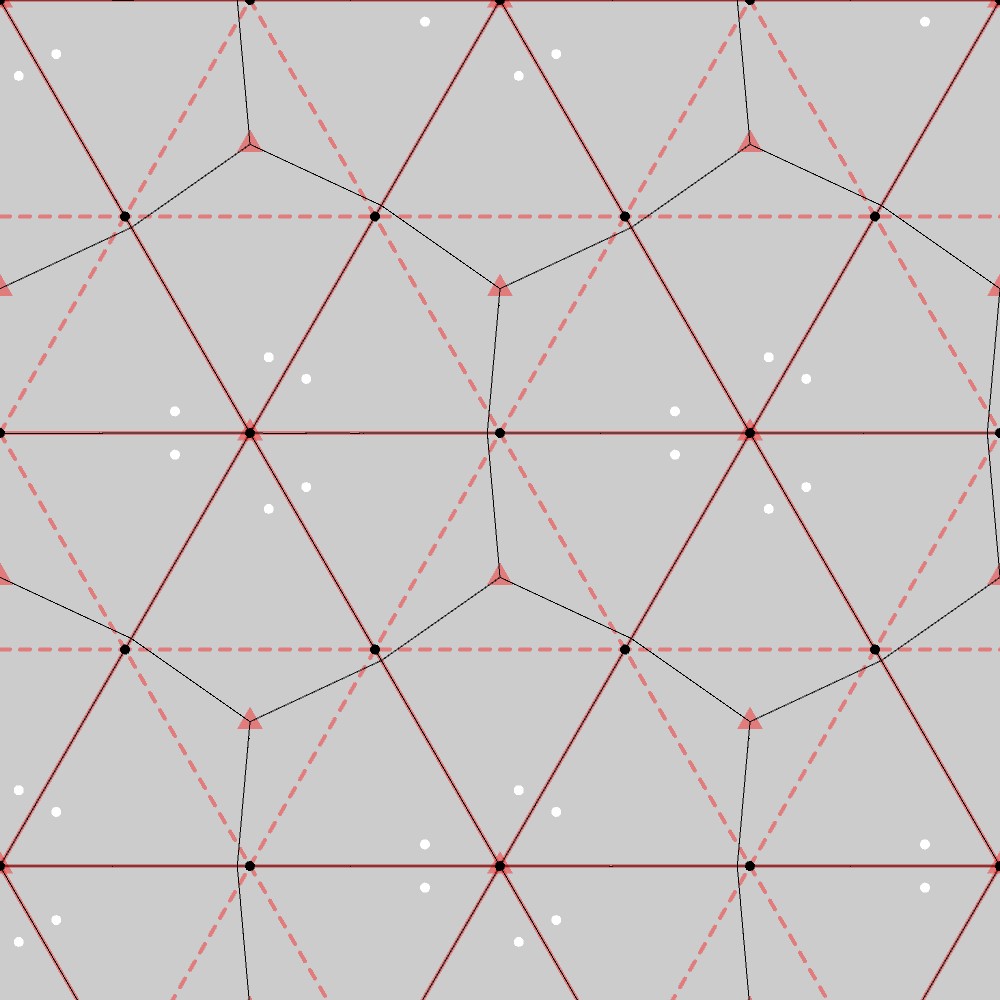
P31M群の基本図形への制約

P31M群によるボロノイ図から、P31M群の基本図形への制約について考えてみます。

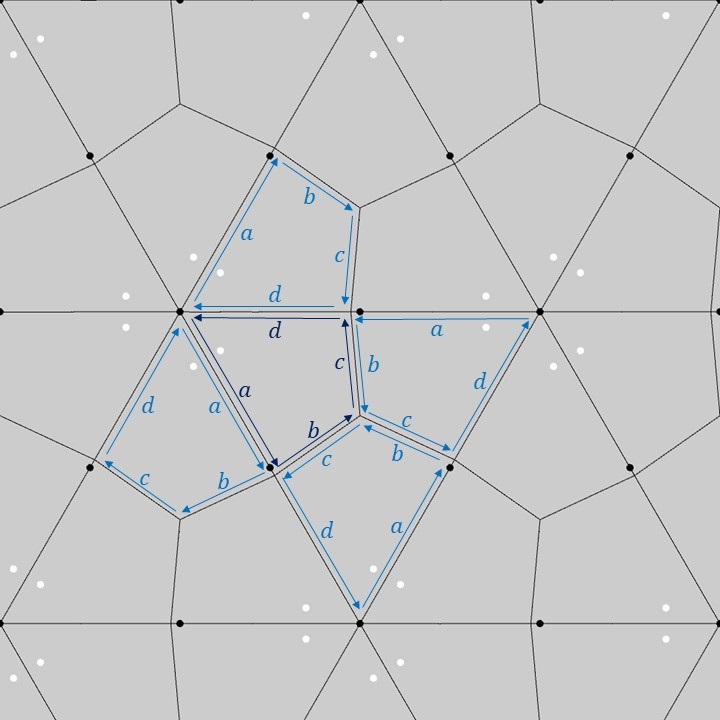
上図のように、１つの基本図形の四角形の各辺に\(a,b,c,d\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を三角格子上でP31M群の対称性に合わせて移動させると、隣り合う四角形に対するラベルは薄い青色のラベルのようになります。隣り合う四角形同士の各辺の対応関係を見てみると、四角形の性質として、辺\(a\)と辺\(d\)のなす角が60°、辺\(b\)と辺\(c\)の長さが等しく、なす角が120°になるように配置されることが分かります。これがP31M群の基本図形に対する制約となっています。

なお、別記事「渦巻き図形」で直観的に選んだP31M群の基本図形は二等辺三角形でした。これは四角形に対して辺\(c\)と辺\(d\)が交わる頂点が辺\(a\)と辺\(d\)が交わる頂点に重なるように辺\(d\)が縮んだ場合と考えることができます。

P6群の基本図形の形状

P6群のボロノイ図

P6群の対称性をもつ母点に対してボロノイ図を作ってみます。

P6群のベースとなる三角格子の形状（黒点）に対して、1つの三角格子点から横隣りの格子点までの距離の3分の1、右斜め下の格子点までの距離の5分の1の長さまで移動した位置にある点（白点）をとり、この点をP6群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

この結果から、P6群の基本図形は五角形になることが分かります。実際、下図に示す通り、この図形は三角格子上で赤丸点を中心とした180°回転、赤三角点を中心とした120°回転および赤六角星形点を中心とした60°回転（P6群の対称性）に対して不変になっています。

P6群の基本図形への制約

P6群によるボロノイ図から、P6群の基本図形への制約について考えてみます。

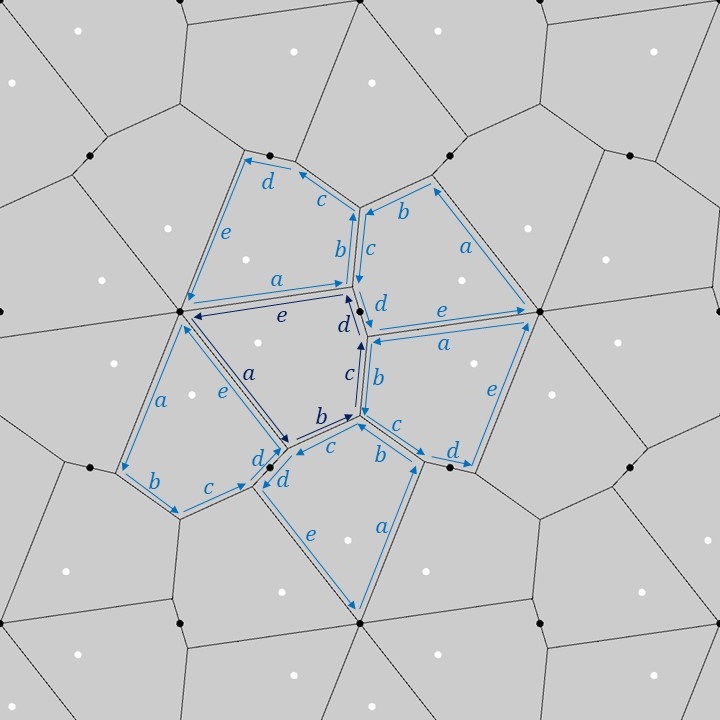
上図のように、１つの基本図形の五角形の各辺に\(a,b,c,d,e\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を三角格子上でP6群の対称性に合わせて移動させると、隣り合う五角形に対するラベルは薄い青色のラベルのようになります。隣り合う五角形同士の各辺の対応関係を見てみると、五角形の性質として、辺\(a\)と辺\(e\)のなす角が60°、辺\(b\)と辺\(c\)の長さが等しく、なす角が120°になるように配置されることが分かります。これがP6群の基本図形に対する制約となっています。

なお、別記事「渦巻き図形」で直観的に選んだP6群の基本図形はカイト形でした。これは五角形に対して辺\(d\)が縮んでその中点に収束した場合と考えることができます。

P6M群の基本図形の形状

P6M群のボロノイ図

P6M群の対称性をもつ母点に対してボロノイ図を作ってみます。

P6M群のベースとなる三角格子の形状（黒点）に対して、1つの三角格子点から横隣りの格子点までの距離の2分の1、右斜め下の格子点までの距離の3分の1の長さまで移動した位置にある点（白点）をとり、この点をP6M群の対称性に合わせて並べていったものを母点としてボロノイ図を描くと、以下の図のようになります。

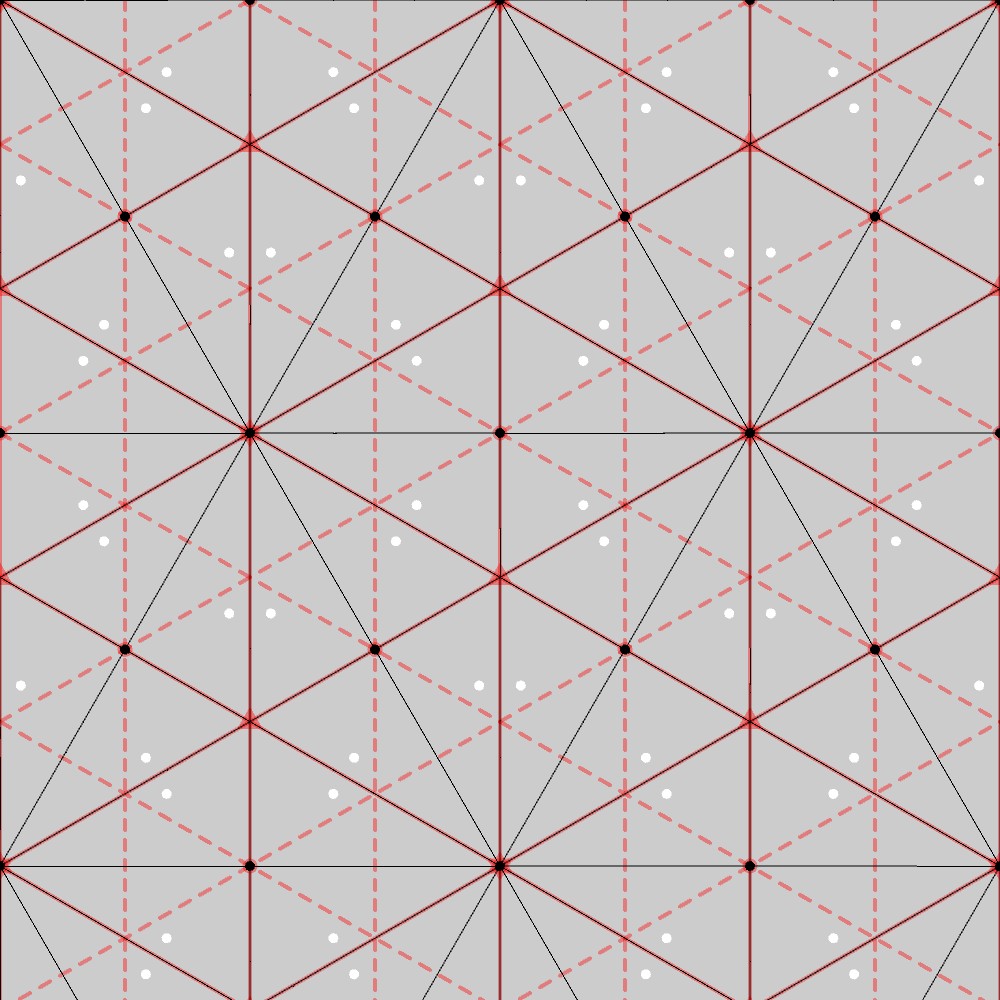
この結果から、P6M群の基本図形は1つの鋭角が30°である直角三角形になることが分かります。実際、下図に示す通り、この図形は三角格子上で縦斜め方向の鏡映変換（赤い線）と滑り鏡映変換（赤い点線）、赤丸点を中心とした180°回転、赤三角点を中心とした120°回転および赤六角星形点を中心とした60°回転（P6M群の対称性）に対して不変になっています。

P6M群の基本図形への制約

P6M群によるボロノイ図から、P6M群の基本図形への制約について考えてみます。

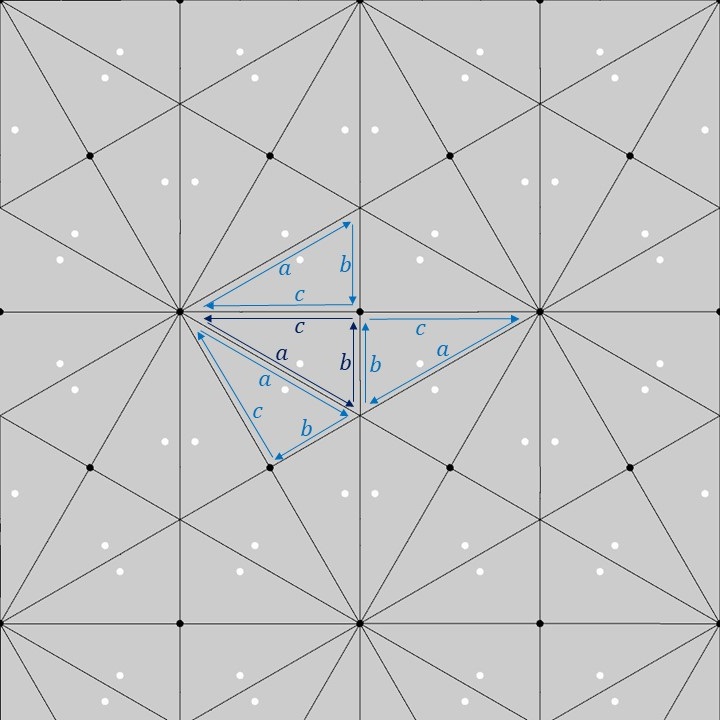
上図のように、１つの基本図形の直角三角形の各辺に\(a,b,c\)のラベルを付けてみます（濃い青色のラベル）。この１つの基本図形を三角格子上でP6M群の対称性に合わせて移動させると、隣り合う直角三角形に対するラベルは薄い青色のラベルのようになります。隣り合う直角三角形同士の各辺の対応関係を見てみると、P6M群の基本図形については1つの鋭角が30°である直角三角形になるという以外、特に制約はないようです。