Contents
トーラス結び目(Torus Knot)
ここでは、書籍「非線形ダイナミクスとカオス」のp.302,303で解説されているトーラス結び目と\(N=3\)でのリサージュ図形との関係を見ていこうと思います。
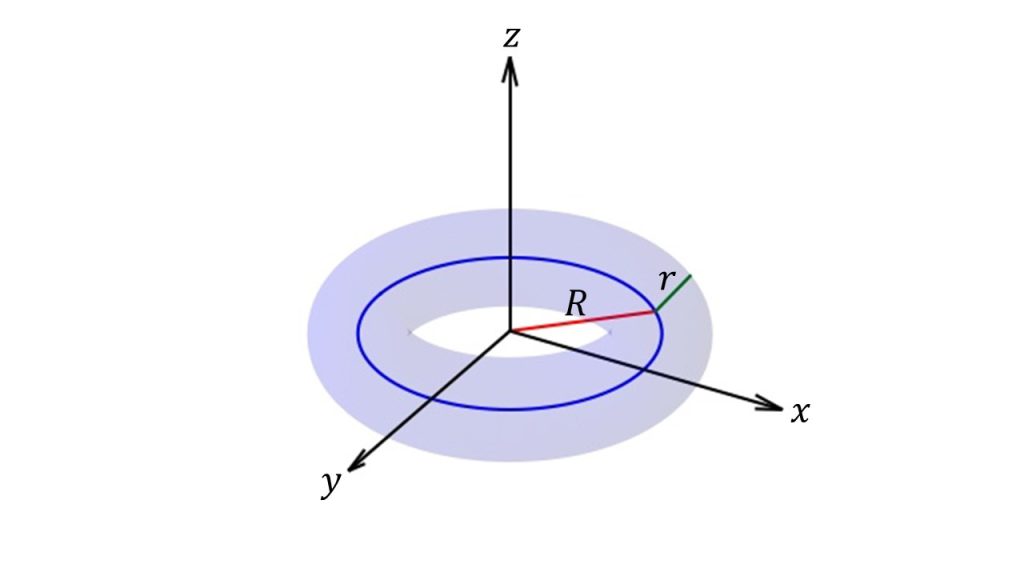
トーラスというのはドーナツ型の立体表面のことです。このトーラス上に糸を巻いていき、最後に糸の端と端を結ぶことでトーラス結び目を作ることができます。つまり、トーラス結び目はトーラス上の閉じた曲線のことです。

トーラス結び目の式
トーラス結び目は次のようにパラメータ表示することができます。
\[ x = (R+r \cos \omega_m t) \cos \omega_M t, \\ y = (R+r \cos \omega_m t) \sin \omega_M t, \\ z = r \sin \omega_m t \]
ここで、\(R\)はトーラスの大半径(major radius)、\(r\)はトーラスの小半径(minor radius)、\(\omega_M\)は大半径方向の周波数、\(\omega_m\)は小半径方向の周波数をそれぞれ表します。
なお、トーラス結び目が作れるのは\(\omega_M/\omega_m\)が有理数のときになります。無理数の場合、上記の式で曲線を描いても閉じることはありません。
トーラス結び目とリサージュ図形の関係
上で示したトーラス結び目の\(x\)方向の式と\(y\)方向の式を変形すると、
\[ x = R \cos \omega_M t + \frac{r}{2} \cos ( \omega_M + \omega_m ) t + \frac{r}{2} \cos (\omega_M – \omega_m) t, \\ y = R \sin \omega_M t + \frac{r}{2} \sin ( \omega_M + \omega_m ) t + \frac{r}{2} \sin (\omega_M – \omega_m) t \]
となります。これらの式と\(N=3\)でのリサージュ曲線の式を比べると、
\[ A_1=B_1=R, \ \ A_2=B_2=\frac{r}{2}, \ \ A_3=B_3=\frac{r}{2}, \\ \omega_{x,1}=\omega_{y,1}=\omega_M, \ \ \omega_{x,2}=\omega_{y,2}=\omega_M+\omega_m, \ \ \omega_{x,3}=\omega_{y,3}=\omega_M-\omega_m, \\ \theta_{x,1}=\theta_{x,2}=\theta_{x,3}=90^{\circ}, \ \ \theta_{y,1}=\theta_{y,2}=\theta_{y,3}=0^{\circ} \]
のように対応付けることができます。つまり、トーラス結び目の\(x, y\)平面への射影は\(N=3\)でのリサージュ曲線とみなすことができます。
トーラス結び目を描く
では、トーラス結び目の \(x, y\)平面への射影を実際に描いてみます。
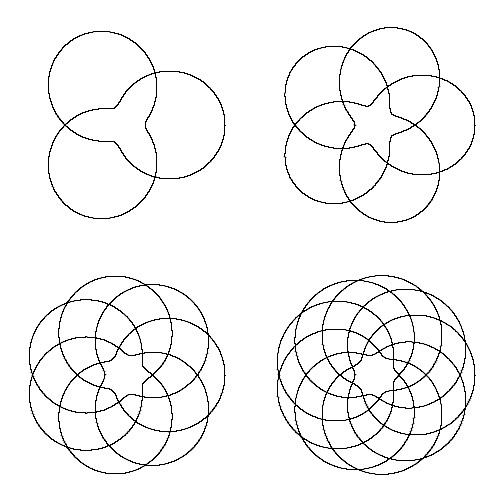
上記の図で\(\omega_M/\omega_m\)はそれぞれ左上が\(2/3\)、右上が \(3/5\)、左下が\(5/7\)、右上が \(7/9\)としています。トーラス結び目はなかなかきれいな模様になりますね。
この図形を描いたときのプログラムコード(Processing)を示しておきます。
void setup(){
size(500,500);
background(255,255,255);
noFill();
float R = 60.0;
float r = 40.0;
// 2:3のトーラス結び目
translate(width/4.0, height/4.0);
float omega_meridian = 2.0; // 経線(大半径)方向の周波数
float omega_longitude = 3.0; // 緯線(小半径)方向の周波数
drawTorusKnot(R,r,omega_meridian,omega_longitude);
// 3:5のトーラス結び目
translate(width/2.0, 0.0);
omega_meridian = 3.0; // 経線(大半径)方向の周波数
omega_longitude = 5.0; // 緯線(小半径)方向の周波数
drawTorusKnot(R,r,omega_meridian,omega_longitude);
// 5:7のトーラス結び目
translate(-width/2.0, height/2.0);
omega_meridian = 5.0; // 経線(大半径)方向の周波数
omega_longitude = 7.0; // 緯線(小半径)方向の周波数
drawTorusKnot(R,r,omega_meridian,omega_longitude);
// 7:9のトーラス結び目
translate(width/2.0, 0.0);
omega_meridian = 7.0; // 経線(大半径)方向の周波数
omega_longitude = 9.0; // 緯線(小半径)方向の周波数
drawTorusKnot(R,r,omega_meridian,omega_longitude);
}
// トーラス結び目を描く関数
void drawTorusKnot(
float R, // トーラスの大半径
float r, // トーラスの小半径
float omega_meridian, // 経線(大半径)方向の周波数
float omega_longitude // 緯線(小半径)方向の周波数
){
int N = 3; // 項数
float[] r1 = new float[3];
r1[0] = R;
r1[1] = r/2.0;
r1[2] = r/2.0;
float[] omega1 = new float[3];
omega1[0] = omega_meridian;
omega1[1] = omega_meridian + omega_longitude;
omega1[2] = omega_meridian - omega_longitude;
float[] theta1_x = {90.0, 90.0, 90.0};
float[] theta1_y = {0.0, 0.0, 0.0};
float cycle1 = 1.0;
drawLissajous(N, r1, omega1, theta1_x, r1, omega1, theta1_y, cycle1);
}
// リサージュ曲線を描く関数
void drawLissajous(
int N, // 項数
float[] r_x, // x方向の振幅に関する配列
float[] omega_x, // x方向の周波数に関する配列
float[] theta_x, // x方向の位相に関する配列
float[] r_y, // y方向の振幅に関する配列
float[] omega_y, // y方向の周波数に関する配列
float[] theta_y, // y方向の位相に関する配列
float cycle // 回転数
){
float x, y;
int num = 10000;
beginShape();
for(int i=0; i<num*cycle; i++){
x = 0.0;
y = 0.0;
for(int j=0; j<N; j++){
x += r_x[j] * sin( omega_x[j] * radians(i*360.0/num) + radians(theta_x[j]) );
y += r_y[j] * sin( omega_y[j] * radians(i*360.0/num) + radians(theta_y[j]) );
}
vertex(x,y);
}
endShape();
}
トーラス結び目を描く(ちょっと3D)
トーラス結び目はトーラス上に巻き付く閉じた曲線ですので、実際は3Dの曲線となります。そこで少しだけ3D感を出せるように、\(z\)軸方向に対して曲線が手前(正の向き)に来るほど線を太く、曲線が奥側(負の向き)に行くほど線を細くして描いてみました。
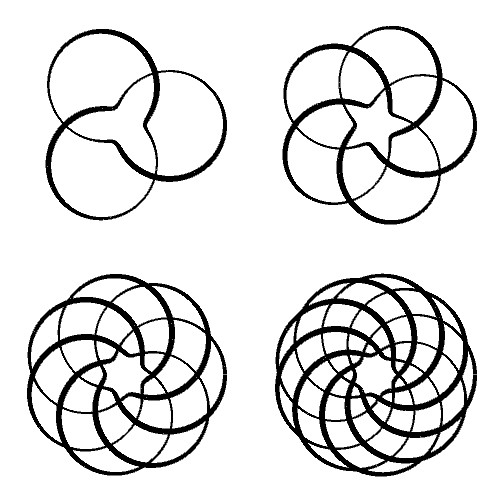
多少遠近感が出て、トーラス結び目らしくなった気がします。
これらの図形を描いたときのプログラムコード(Processing)を示しておきます。
void setup(){
size(500,500,P3D);
background(255,255,255);
noFill();
ortho();
float R = 60.0;
float r = 40.0;
float omega_meridian = 2.0; // 経線(大半径)方向の周波数
float omega_longitude = 3.0; // 緯線(小半径)方向の周波数
translate(width/4.0, height/4.0, 0.0);
drawTorusKnot(R,r,omega_meridian,omega_longitude);
omega_meridian = 3.0; // 経線(大半径)方向の周波数
omega_longitude = 5.0; // 緯線(小半径)方向の周波数
translate(2.0*width/4.0, 0.0, 0.0);
drawTorusKnot(R,r,omega_meridian,omega_longitude);
omega_meridian = 5.0; // 経線(大半径)方向の周波数
omega_longitude = 7.0; // 緯線(小半径)方向の周波数
translate(-2.0*width/4.0, 2.0*height/4.0, 0.0);
drawTorusKnot(R,r,omega_meridian,omega_longitude);
omega_meridian = 7.0; // 経線(大半径)方向の周波数
omega_longitude = 9.0; // 緯線(小半径)方向の周波数
translate(2.0*width/4.0, 0.0, 0.0);
drawTorusKnot(R,r,omega_meridian,omega_longitude);
save("torus_knot_3D.jpg");
}
// トーラス結び目を描く関数
void drawTorusKnot(
float R, // トーラスの大半径
float r, // トーラスの小半径
float omega_meridian, // 経線(大半径)方向の周波数
float omega_longitude // 緯線(小半径)方向の周波数
){
int N = 3; // 項数
stroke(0,0,0);
float[] r1 = new float[3];
r1[0] = R;
r1[1] = r/2.0;
r1[2] = r/2.0;
float[] r1_z = new float[3];
r1_z[0] = r;
r1_z[1] = 0.0;
r1_z[2] = 0.0;
float[] omega1 = new float[3];
omega1[0] = omega_meridian;
omega1[1] = omega_meridian + omega_longitude;
omega1[2] = omega_meridian - omega_longitude;
float[] omega1_z = new float[3];
omega1_z[0] = omega_longitude;
omega1_z[1] = 0.0;
omega1_z[2] = 0.0;
float[] theta1_x = {90.0, 90.0, 90.0};
float[] theta1_y = {0.0, 0.0, 0.0};
float[] theta1_z = {0.0, 0.0, 0.0};
float cycle1 = 1.0;
drawLissajous_3D(N, r1, omega1, theta1_x, r1, omega1, theta1_y, r1_z, omega1_z, theta1_z, cycle1);
}
// リサージュ曲線を描く関数(3Dバージョン)
void drawLissajous_3D(
int N, // 項数
float[] r_x, // x方向の振幅に関する配列
float[] omega_x, // x方向の周波数に関する配列
float[] theta_x, // x方向の位相に関する配列
float[] r_y, // y方向の振幅に関する配列
float[] omega_y, // y方向の周波数に関する配列
float[] theta_y, // y方向の位相に関する配列
float[] r_z, // z方向の振幅に関する配列
float[] omega_z, // z方向の周波数に関する配列
float[] theta_z, // z方向の位相に関する配列
float cycle // 回転数
){
float x, y, z;
int num = 10000;
beginShape();
for(int i=0; i<num*cycle; i++){
x = 0.0;
y = 0.0;
z = 0.0;
for(int j=0; j<N; j++){
x += r_x[j] * sin( omega_x[j] * radians(i*360.0/num) + radians(theta_x[j]) );
y += r_y[j] * sin( omega_y[j] * radians(i*360.0/num) + radians(theta_y[j]) );
z += r_z[j] * sin( omega_z[j] * radians(i*360.0/num) + radians(theta_z[j]) );
}
strokeWeight(2.0*(z+2.0*r_z[0])/r_z[0]);
vertex(x,y,z);
}
endShape();
}