反復関数

  1. ホーム
  2. フラクタル
  3. 反復関数

ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.18,19に掲載されている、反復関数を用いた4つの図形を描いてみました。

反復関数を用いたシェルピンスキーのギャスケット

今回描いた反復関数を用いたシェルピンスキーのギャスケットです。

反復関数を用いたシェルピンスキーのギャスケット

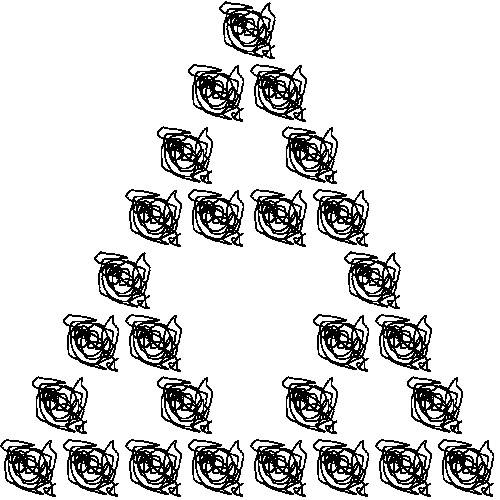
適当に描いた画像を用意して、以下の3つの反復関数を利用してシェルピンスキーのギャスケットの形に並べています。今回は反復回数を3回だけにしています。こうやって並べてみると、なんかきれいな図形にみえてくるので不思議です。

なお、シェルピンスキーのギャスケットは別記事「カーペット」でも紹介しています。

シェルピンスキーのギャスケットに対する反復関数

画像に対して、図のように\(x\)軸と\(y\)軸を取り、画像の縦横の長さを\(l\)とすると、シェルピンスキーのギャスケットを生成するための3つの反復関数は以下のようになります。\[ \begin{align} f_1 &: x \to \frac{l}{4}+\frac{x}{2}, \ \ y \to \frac{y}{2} \\ f_2 &: x \to \frac{x}{2}, \ \ y \to \frac{l}{2}+\frac{y}{2} \\ f_3 &: x \to \frac{l}{2}+\frac{x}{2}, \ \ y \to \frac{l}{2}+\frac{y}{2} \end{align} \]

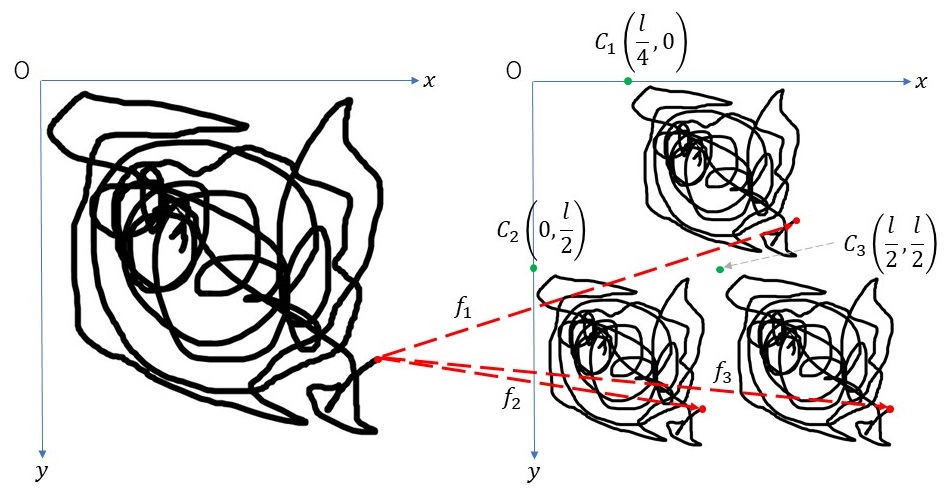
シェルピンスキーのギャスケットを生成するための3つの反復関数

図で見れば、元の画像（上図左）のサイズを縦横半分にしたものを生成し、右図の\(C_1, C_2, C_3\)が左上の座標となるように図形を並べていく処理を繰り返しているだけになります。

プログラムコード

今回作成した反復関数を用いたシェルピンスキーのギャスケットのプログラムコードを示します。

int iteration_num = 3; // 反復回数 

void setup(){
  size(500,500);
  background(255,255,255);
//  translate(width/2.0, height/2.0);

  // オリジナル画像を取り込む
  PImage img = loadImage("hoge.jpg");
  image(img, 0.0, 0.0, width, height);
  
  int iter = 0;
  while(iter<iteration_num){
    // 描いた図形を一旦imgに保存する
    img = createImage(width, height, RGB);
    loadPixels();
    for(int j=0; j<img.height; j++){
      for(int i=0; i<img.width; i++){
        img.set(i, j, pixels[j*width + i]);
      }
    }
    background(255,255,255);
    // imgの画素が黒色の場合、4つの反復変換を行ってコッホ曲線を更新していく
    for(int j=0; j<img.height; j++){
      for(int i=0; i<img.width; i++){
        if(img.get(i,j) == color(0,0,0)){
          rect(width/4.0+0.5*i, 0.5*j, 0.1, 0.1);
          rect(0.5*i, width/2.0+0.5*j, 0.1, 0.1);
          rect(width/2.0+0.5*i, width/2.0+0.5*j, 0.1, 0.1);
        }
      }
    }
    iter++;
  }
}

反復関数を用いたコッホ曲線

次は、反復関数を用いたコッホ曲線です。

反復関数を用いたコッホ曲線

コッホ曲線は別記事「コッホ雪片」でも紹介しています。

コッホ曲線に対する反復関数

最初に一本の線分（長さ\(l\)）を描き、図のように\(x\)軸と\(y\)軸をとると、コッホ曲線を生成するための4つの反復関数は以下のようになります。\[ \begin{align} f_1 &: x \to 0.33 x, \ \ y \to 0.33y \\ f_2 &: x \to 0.17x-0.29y+0.33l, \ \ y \to 0.29x+0.17y \\ f_3 &: x \to 0.17x+0.29y+0.5l, \ \ y \to -0.29x+0.17y+0.29l \\ f_4 &: x \to 0.33x+0.67l, \ \ y \to 0.33y \end{align} \]

コッホ曲線を生成するための4つの反復関数

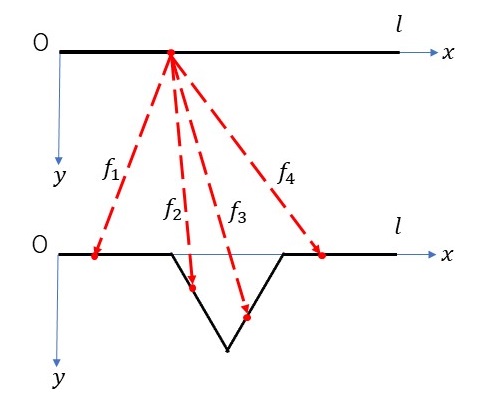
なお、ここでは反復関数の各係数として書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.19に掲載されているパラメータをそのまま利用しました。ただし、係数\(e\)と\(f\)に関しては最初の線分の長さ\(l\)を掛ける必要があります。

プログラムコード

今回作成した反復関数を用いたコッホ曲線のプログラムコードを示します。

int iteration_num = 4; // 反復回数 

void setup(){
  size(600,200);
  background(255,255,255);

  // 直線を描画する
  line(0.0, 0.0, width, 0.0); 
  
  PImage img;
  int iter = 0;
  while(iter<iteration_num){
    // 描いた図形を一旦imgに保存する
    img = createImage(width, height, RGB);
    loadPixels();
    for(int j=0; j<img.height; j++){
      for(int i=0; i<img.width; i++){
        img.set(i, j, pixels[j*width + i]);
      }
    }
    background(255,255,255); // キャンバスを白色で塗りつぶす
    // imgの画素が黒色の場合、4つの反復変換を行ってコッホ曲線を更新していく
    for(int j=0; j<img.height; j++){
      for(int i=0; i<img.width; i++){
        if(img.get(i,j) == color(0,0,0)){
          rect(0.33*i, 0.33*j, 1.0, 1.0);
          rect(0.17*i-0.29*j+0.33*width, 0.29*i+0.17*j, 1.0, 1.0);
          rect(0.17*i+0.29*j+0.5*width, -0.29*i+0.17*j+0.29*width, 1.0, 1.0);
          rect(0.33*i+0.67*width, 0.33*j, 1.0, 1.0);
        }
      }
    }
    iter++;
  }
}

反復関数を用いたレヴィC曲線

次は、反復関数を用いたレヴィＣ曲線です。

反復関数を用いたレヴィＣ曲線

レヴィＣ曲線は別記事「Ｌシステム」でも紹介しています。

レヴィＣ曲線に対する反復関数

下図のように横の長さが\(l\)となるキャンバス（グレーの領域）に対して\(x\)軸と\(y\)軸をとります。そのキャンバス上に点C\((\frac{l}{4},\frac{l}{4})\)をとり、点Cを左端とする長さ\(\frac{l}{2}\)の線分を取ります。この線分を最初の起点として、レヴィＣ曲線を生成するための2つの反復関数は以下のようになります。\[ \begin{align} f_1 &: x \to \frac{1}{2} (x-\frac{l}{4})-\frac{1}{2} (y-\frac{l}{4}) + \frac{l}{4}, \ \ y \to \frac{1}{2} (x-\frac{l}{4})+\frac{1}{2} (y-\frac{l}{4}) + \frac{l}{4} \\ f_2 &: x \to \frac{1}{2} (x-\frac{l}{4})+\frac{1}{2} (y-\frac{l}{4}) + \frac{l}{2}, \ \ y \to -\frac{1}{2} (x-\frac{l}{4})+\frac{1}{2} (y-\frac{l}{4}) + \frac{l}{2} \end{align} \]

レヴィＣ曲線を生成するための2つの反復関数

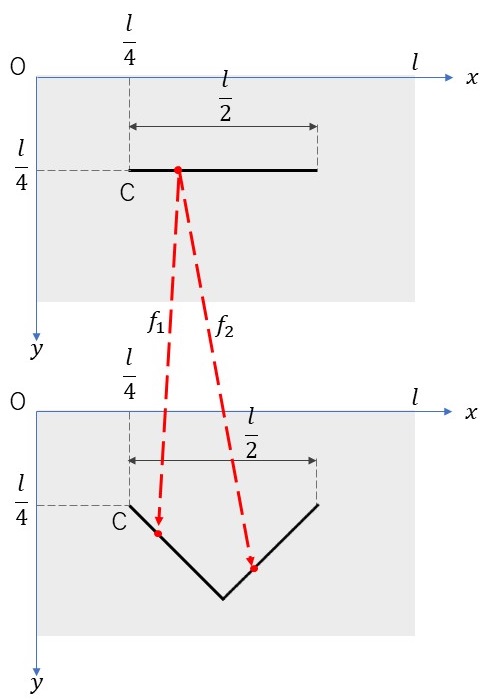
プログラムコード

今回作成した反復関数を用いたレビィＣ曲線のプログラムコードを示します。

int iteration_num = 20; // 反復回数 

void setup(){
  size(600,600);
  background(255,255,255);

  PVector center = new PVector(width/4.0, height/4.0); // 原点の座標
  float len = width/2.0; // 最初に与える線分の長さ

  // 直線を描画する
  line(center.x, center.y, center.x + len, center.y); 
  
  PImage img;
  int iter = 0;
  while(iter<iteration_num){
    // 描いた図形を一旦imgに保存する
    img = createImage(width, height, RGB);
    loadPixels();
    for(int j=0; j<img.height; j++){
      for(int i=0; i<img.width; i++){
        img.set(i, j, pixels[j*width + i]);
      }
    }
    background(255,255,255); // キャンバスを白色で塗りつぶす
    // imgの画素が黒色の場合、2つの反復変換を行ってレヴィC曲線を更新していく
    for(int j=0; j<img.height; j++){
      for(int i=0; i<img.width; i++){
        if(img.get(i,j) == color(0,0,0)){
          rect(center.x + 0.5*(i-center.x) - 0.5*(j-center.y), center.y + 0.5*(i-center.x) + 0.5*(j-center.y), 0.1, 0.1);
          rect(center.x + 0.5*(i-center.x) + 0.5*(j-center.y) + 0.5*len, center.y - 0.5*(i-center.x) + 0.5*(j-center.y) + 0.5*len, 0.1, 0.1);
        }
      }
    }
    iter++;
  }
}

反復関数を用いた雪片

次は、反復関数を用いた雪片です。

反復関数を用いた雪片

雪片に対する反復関数

下図のように縦横の長さが\(l\)となるキャンバス（グレーの領域）に対して\(x\)軸と\(y\)軸をとります。そのキャンバス上の中央点\((\frac{l}{2},\frac{l}{2})\)から長さ\(\frac{2}{5}l\)の線分を放射状に6本取ります。これらの線分を最初の起点として、雪片を生成するための2つの反復関数は以下のようになります。\[ \begin{align} f_1 &: x \to \left( \frac{4}{5} \right)^{\frac{1}{6}} \left( \frac{1}{2} (x-\frac{l}{2})-\frac{\sqrt{3}}{2} (y-\frac{l}{2}) \right) + \frac{l}{2}, \ \ y \to \left( \frac{4}{5} \right)^{\frac{1}{6}} \left( \frac{\sqrt{3}}{2} (x-\frac{l}{2})+\frac{1}{2} (y-\frac{l}{2}) \right) + \frac{l}{2} \\ f_2 &: x \to \frac{1}{5} (x-\frac{l}{2}) + \frac{l}{2}, \ \ y \to \frac{1}{5} (y-\frac{l}{2}) + \frac{l}{10} \end{align} \]

雪片を生成するための2つの反復関数

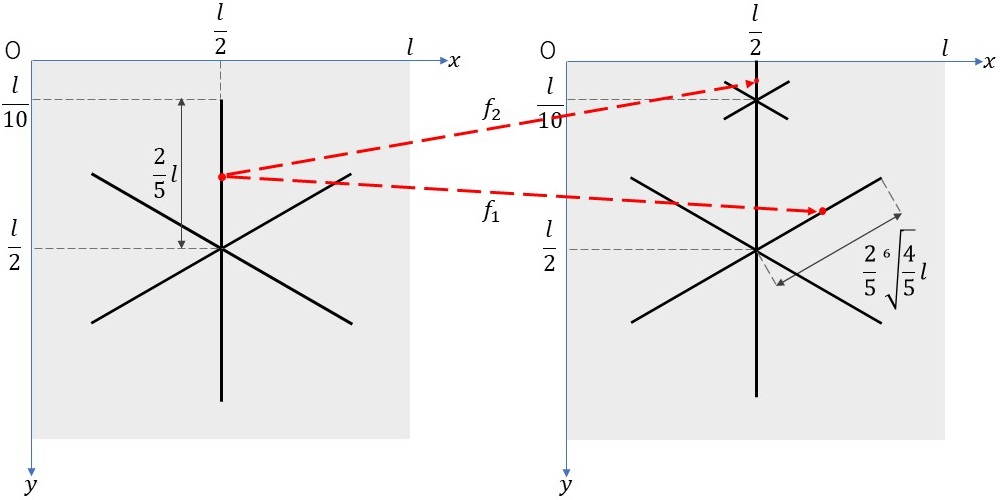
図で見ると、反復関数\(f_1\)は元の画像（上図左）のサイズを\( \left( \frac{4}{5} \right)^{\frac{1}{6}} \)倍して60°回転したものであり、反復関数\(f_2\)は元の画像のサイズを\(\frac{1}{5}\)倍して中心が\( (\frac{l}{2}, \frac{l}{10}) \)となるように移動したものになります。

プログラムコード

今回作成した反復関数を用いた雪片のプログラムコードを示します。縮小比率をうまく調整すればもっときれいな雪片を描くことができそうです。

int iteration_num = 100; // 反復回数 

void setup(){
  size(1000,1000);
  background(255,255,255);

  PVector center = new PVector(width/2.0, height/2.0); // 原点の座標
  float len = width*2.0/5.0; // 正六角形の一辺の長さ
  float ratio = pow(4.0/5.0, 1.0/6.0);
  float ratio2 = 1.0/5.0;

  // 正六角形型に線分を描く
  fill(0,0,0);
  for(int i=0; i<6; i++){
    PVector temp = PVector.fromAngle(radians(-90+60*i)).mult(len);
    line(center.x, center.y, center.x + temp.x, center.y + temp.y); 
  }
 
  PImage img;
  int iter = 0;
  while(iter<iteration_num){
    // 描いた図形を一旦imgに保存する
    img = createImage(width, height, RGB);
    loadPixels();
    for(int j=0; j<img.height; j++){
      for(int i=0; i<img.width; i++){
        img.set(i, j, pixels[j*width + i]);
      }
    }
    background(255,255,255); // キャンバスを白色で塗りつぶす
    // imgの画素が黒色の場合、2つの反復変換を行って雪片を更新していく
    for(int j=0; j<img.height; j++){
      for(int i=0; i<img.width; i++){
        if( img.get(i,j) != color(255,255,255) ){
          rect(center.x + ((i-center.x)/2.0 - (j-center.y)*sqrt(3.0)/2.0)*ratio, center.y + ((i-center.x)*sqrt(3.0)/2.0 + (j-center.y)/2.0)*ratio, 0.1, 0.1);
          rect(width/2.0 + (i-center.x)*ratio2, height/10.0 + (j-center.y)*ratio2, 0.1, 0.1);
        }
      }
    }
    iter++;
  }
}

コメントを残す