ここでは、15タイプある五角形によるタイリングのうち、Type 6のタイリングを再現してみました。なお、今回のタイリングを作成するにあたって、杉本晃久さんのサイトで紹介されている「凸五角形タイル張り問題」を参考にしました。
Contents
五角形によるタイリング(Type 6)
今回、再現した五角形によるタイリング(Type 6)は以下のような図形になります。

以下で、この五角形によるタイリング(Type 6)の描き方について解説していきます。
五角形によるタイリング(Type 6)の描き方
対称性について
まず、この五角形によるタイリング(Type 6)の対称性について考えます。

上図のように、タイリングのパターンをじっくり見ていくと、上図の赤丸の周りの180°回転に対して図形は回転対称になっていることが分かります。また、黒色の点を格子としてみると、近接する4つの黒色の点同士が平行四辺形を形作っていることから、黒色の点は一般格子になっていることが分かります。これらをまとめると、五角形によるタイリング(Type 6)は、壁紙群P2の対称性を持つことが分かります。さらに言えば、アイソヘドラルタイリングIH4(P2)に分類されます。
五角形の準備
今回利用する五角形は以下のような図形になります。

五角形の角度のうち、上図の角度A,B,Dの和が360°、角度Aが角度Cの2倍になるようにとります。また、辺ABと辺AEと辺DE、および辺CBと辺CDの長さがそれぞれ同じになるようにとります。
この五角形を描くために、以下のように五角形を分割すると分かりやすくなります。
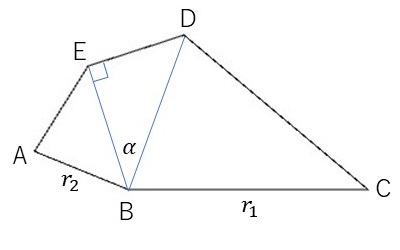
ポイントは、△BEDが直角三角形になることです。これは
- A+B+D=360°より、C+E=180°
- △ABEが二等辺三角形だから、∠AEB=90°-A/2=90°-C
- よって、∠BED=E-∠AEB=(180°-C)-(90°-C)=90°
となることから分かります。
そして、辺CBの長さを\(r_1\)、辺ABの長さを\(r_2\)とおき、∠DBEを\(\alpha\)とおきます。このとき、△CBDは二等辺三角形なので、辺BDの長さは\(2 r_1 \sin \frac{C}{2} \)となり、△ABEが二等辺三角形なので、辺BEの長さは\(2 r_2 \sin \frac{A}{2} = 2r_2 \sin C \)となります。あと、辺DEの長さは\(r_2\)で、△BEDが直角三角形であることから、\[ 2 r_1 \sin \frac{C}{2} \cos \alpha = 2 r_2 \sin C, \ \ r_2 = 2 r_1 \sin \frac{C}{2} \sin \alpha \]となります。これらを整理すると、\[ \tan \alpha = \frac{1}{2 \sin C}, \ \ r_2 = 2 r_1 \sin \frac{C}{2} \sin \alpha \]となります。つまり、Type 6の五角形は頂点Cの角度と辺BCの長さを指定することで描くことができます。
基本図形の準備
次に、基本図形を準備します。今回は、以下のような組合せを基本図形とします(組合せは他にもあります)。
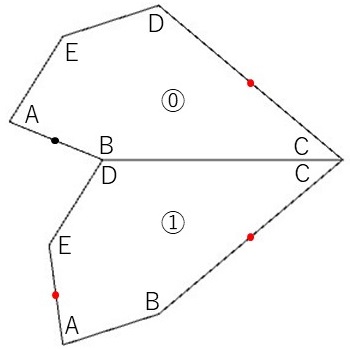
この基本図形を実際に描いていくための手順を示しておきます。
- ⓪の図形を描きます。
- ⓪の五角形の頂点Cの周りで反時計回りに角度Cだけ回転することで①の五角形を描きます。
なお、壁紙群P2の対称性に合わせて基本図形を並べていく際に、今回は⓪の五角形の頂点AとBの中点(上図の黒丸)を一般格子点と合うようにしています。また、⓪の五角形の頂点CとDの中点、①の五角形の頂点EとAの中点、および①の五角形の頂点BとCの中点(いずれも上図の赤丸)を隣り合う一般格子点同士の中点と一致するようにします。
一般格子の準備
上記で説明したように、上図の黒丸や赤丸がそれぞれ一般格子点や隣り合う一般格子点同士の中点と一致するようにとりますので、それに伴い、一般格子の形状も決まってきます。つまり、一般格子を張る2つのベクトルは、⓪の五角形の頂点AとBの中点から⓪の五角形の頂点CとDの中点へのベクトルを2倍したものと、⓪の五角形の頂点AとBの中点から①の五角形の頂点EとAの中点へのベクトルを2倍したものとになります。
壁紙群P2の対称性に合わせて並べる
ここまで準備ができたら、あとは壁紙群P2の対称性に合わせて基本図形を並べていくことで五角形によるタイリングを行うことができます。
ソースコード
今回再現した五角形によるタイリング(Type 6)のプログラムのソースコードを示しておきます。
PVector[][] lattice; // 格子点ベクトル
PShape tile; // タイル
float pentagon_size = 200.0; // 五角形の基準サイズ
float pentagon_angle = 40.0; // Type 6の五角形の標準角度(頂点Cの角度)
PVector[][] v = new PVector[2][5]; // 基本図形を構成する2つの五角形の座標
PVector[] base = new PVector[2]; // 格子を張るベクトル
void setup(){
size(1000, 1000, P2D);
noFill();
makeTileP2(); // タイルを生成
makeGeneralVector(); // 一般格子を張るベクトルの生成
makeLattice(); // 格子点ベクトルを生成
drawTiling(); // タイリングを描画
}
// 五角形の頂点を取得する関数
PVector[] getPentagon(){
float A, B, C, D, E;
C = radians(pentagon_angle);
float alpha = atan( 1.0 / 2.0 / sin(C) );
float r1 = pentagon_size;
float r2 = 2.0 * r1 * sin(C / 2.0) * sin(alpha);
A = 2.0 * C;
B = (radians(90.0) - A / 2.0) + alpha + (radians(90.0) - C / 2.0);
D = (radians(90.0) - C / 2.0) + (radians(90.0) - alpha);
E = radians(90.0) + (radians(90.0) - A / 2.0);
PVector[] v = new PVector[6];
v[0] = PVector.fromAngle(-B).mult(r2/2.0);
v[1] = v[0].copy().rotate(radians(180.0));
v[2] = v[1].copy().add( PVector.fromAngle(radians(0.0)).mult(r1));
v[3] = v[2].copy().add( PVector.fromAngle(-(radians(180.0) - C)).mult(r1) );
v[4] = v[0].copy().add(v[1].copy().sub(v[0].copy()).rotate(-A));
return v;
}
// 五角形を指定された点の周りで回転する関数
PVector[] getRotation(
PVector[] v, // 回転する元の図形の頂点座標
int index, // 回転軸の座標位置のindex
float angle // 回転角度
){
PVector[] rot = new PVector[5];
for(int i=0; i<5; i++){
PVector temp = v[i].copy().sub(v[index].copy());
PVector p = temp.copy().rotate(radians(angle));
rot[i] = v[index].copy().add(p.copy());
}
return rot;
}
// 2つの五角形から構成される基本図形を生成する関数
PShape makeFundamentalShape(){
// 2つの五角形のそれぞれの座標を取得
v[0] = getPentagon();
v[1] = getRotation(v[0], 2, -pentagon_angle);
// 五角形を2つ描いて1つのグループにまとめる
PShape pentagons = createShape(GROUP);
for(int i=0; i<2; i++){
PShape pentagon = createShape();
pentagon.beginShape();
for(int j=0; j<5; j++){
pentagon.vertex(v[i][j].x, v[i][j].y);
}
pentagon.endShape(CLOSE);
pentagons.addChild(pentagon);
}
return pentagons;
}
// タイルを生成する関数
void makeTileP2(){
tile = createShape(GROUP); // PShapeのグループを作る
for(int i=0; i<2; i++){
PShape pentagons = makeFundamentalShape(); // 2つの五角形で構成される図形の生成
pentagons.rotate(PI * i); // 180度回転
tile.addChild(pentagons); // グループに追加
}
}
// 一般格子を張るベクトルを生成する関数
// 基本図形のサイズから算出する
void makeGeneralVector(){
base[0] = v[0][2].copy().add( v[0][3].copy().sub(v[0][2].copy()).mult(0.5) ).mult(2.0);
base[1] = v[1][0].copy().add( v[1][4].copy().sub(v[1][0].copy()).mult(0.5) ).mult(2.0);
}
// 一般格子を生成する関数
void makeLattice(){
int col_num = ceil(width / abs(base[0].x)) + 1; // 列数
int row_num = ceil(height / abs(base[1].y)) + 2; // 行の数
lattice = new PVector[col_num][row_num];
for (int i = 0; i < col_num; i++){
for (int j = 0; j < row_num; j++){
PVector v = PVector.mult(base[0], i);
v.add(PVector.mult(base[1], j));
lattice[i][j] = v.copy();
}
}
}
// 格子形状に合わせたタイリングを描画する関数
void drawTiling(){
// background(255);
for (int i=0; i<lattice.length; i++){
for (int j=0; j<lattice[0].length; j++){
tile.resetMatrix();
tile.translate(lattice[i][j].x, lattice[i][j].y); // タイルの位置を指定
shape(tile); // タイルを描画
}
}
}