ここでは、15タイプある五角形によるタイリングのうち、Type 2のタイリングを再現してみました。なお、今回のタイリングを作成するにあたって、杉本晃久さんのサイトで紹介されている「凸五角形タイル張り問題」を参考にしました。
Contents
五角形によるタイリング(Type 2)
今回、再現した五角形によるタイリング(Type 2)は以下のような図形になります。

以下で、この五角形によるタイリング(Type 2)の描き方について解説していきます。
五角形によるタイリング(Type 2)の描き方
対称性について
まず、この五角形によるタイリング(Type 2)の対称性について考えます。
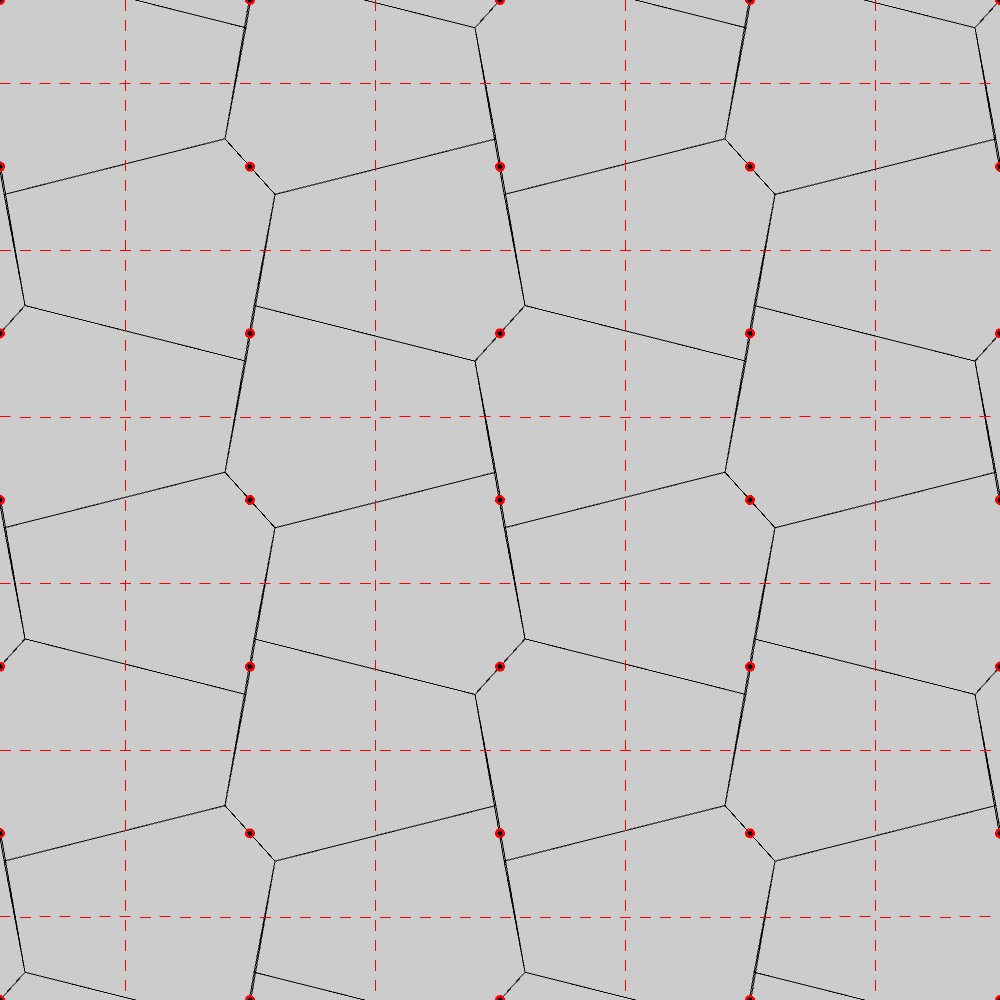
上図のように、タイリングのパターンをじっくり見ていくと、上図の赤丸の周りの180°回転に対して図形は回転対称になっていることが分かり、そして縦横の赤色の点線の軸に対して図形はすべり鏡映を持っていることがわかります。また、黒色の点を格子としてみると、近接する4つの黒色の点同士が長方形を形作っていることから、黒色の点は長方格子になっていることが分かります。これらをまとめると、五角形によるタイリング(Type 2)は、壁紙群PGGの対称性を持つことが分かります。さらに言えば、アイソヘドラルタイリングIH27(PGG)に分類されます。
五角形の準備
今回利用する五角形は以下のような図形になります。
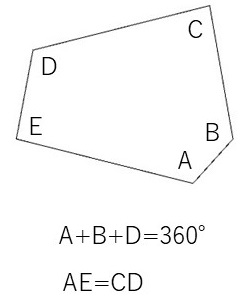
五角形の角度のうち、上図のA, B, Dの和が360°になるようにとります。また、辺AEと辺CDの長さが同じになるようにとります。
ただ、これらの条件についてバランスを取りながら五角形を描いていくことは結構骨の折れる作業だと思います。そこで、ここでは下図のように長方格子を基準にして描くことにしました。
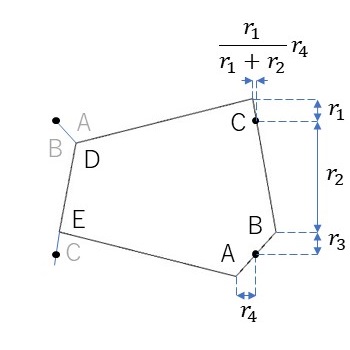
- 黒色の4つの点が近接する長方格子点です。右下の長方格子点が辺ABの中点となるようにします。このとき、辺ABの中点と点Aの距離を幅\(r_4\)、高さ\(r_3\)で表します。
- 辺BCを右上の長方格子点を通るように設定します。このとき、点Cは右上の長方格子点から高さ\(r_1\)となるようにとります。また、点Bと右上の長方格子点との間の高さを\(r_2\)と取ります。
- 点Dを左上の長方格子点から幅\(r_4\)、高さ\(r_3\)の位置にとります。また、点Eを左下の長方格子点から幅\(\frac{r_1}{r_1+r_2}r_4\)、高さ\(r_1\)の位置にとります。
- このようにして得られた頂点A,B,C,D,Eを順に線分で結んでいくと、Type 2の五角形を得ることができます。
基本図形の準備
五角形によるタイリング(Type 2)の基本図形は、Type 2の五角形そのものになります。なお、今回は\(r_1, r_2, r_3\)をそれぞれ縦方向に近接する長方格子点間の距離の\(1/6, 5/6, 1/6\)の長さとなるようにとり、\(r_4\)を横方向に近接する長方格子点間の距離の\(1/10\)の長さとなるようにとりました。
壁紙群PGGの対称性に合わせて並べる
ここまで準備ができたら、あとは壁紙群PGGの対称性に合わせて基本図形を並べていくことで五角形によるタイリング(Type 2)を行うことができます。
ソースコード
今回再現した五角形によるタイリング(Type 2)のプログラムのソースコードを示しておきます。
PVector[][] lattice; // 格子点ベクトル
PShape tile; // タイル
PVector[] base = new PVector[2]; // 格子を張るベクトル
int col_num = 6; // 描画するタイルの列の数
float scalar; // タイルの辺の長さ
void setup(){
size(1000, 1000, P2D);
noFill();
scalar = width * 1.0 / col_num; // 描画ウィンドウと行の数からタイルの大きさを決定
makeRectVector(); // 長方格子を張るベクトルの生成
makeLattice(); // 格子点ベクトルを生成
makeTilePGG(); // タイルを生成
drawTiling(); // タイリングを描画
}
// 長方格子を張るベクトルを生成する関数
void makeRectVector(){
base[0] = new PVector(1.0, 0.0);
base[1] = PVector.fromAngle(PI / 2.0);
base[0].mult(1.5);
}
// 長方格子を生成する関数
void makeLattice(){
int row_num = ceil(col_num / base[1].y); // 行の数
lattice = new PVector[col_num + 1][row_num + 1];
for (int i = 0; i < col_num + 1; i++){
for (int j = 0; j < row_num + 1; j++){
PVector v = PVector.mult(base[0], i * scalar);
v.add(PVector.mult(base[1], j * scalar));
lattice[i][j] = new PVector(v.x , v.y);
}
}
}
// 五角形を生成する関数(基本図形)
PShape makePentagon(){
PVector[] v = new PVector[5]; // 五角形の頂点
float r1, r2, r3, r4;
r1 = 1.0/6.0 * scalar * base[1].y;
r2 = 5.0/6.0 * scalar * base[1].y;
r3 = 1.0/6.0 * scalar * base[1].y;
r4 = 1.0/10.0 * scalar * base[0].x;
v[0] = new PVector(-r4, r3);
v[1] = new PVector(r4, -r3);
v[2] = new PVector(-r4 * r1 / (r1 + r2), -scalar * base[1].y - r1);
v[3] = new PVector(-scalar * base[0].x + r4, -scalar * base[1].y + r3);
v[4] = new PVector(-scalar * base[0].x + r4 * r1 / (r1 + r2), -r1);
// 五角形を描く
PShape pentagon = createShape();
pentagon.beginShape();
for(int i=0; i<5; i++){
pentagon.vertex(v[i].x, v[i].y);
}
pentagon.endShape(CLOSE);
return pentagon;
}
// タイルを生成する関数
void makeTilePGG(){
tile = createShape(GROUP); // PShapeのグループを作る
PShape pentagon = makePentagon(); // 五角形の生成
tile.addChild(pentagon); // グループに追加
pentagon = makePentagon(); // 五角形の生成
pentagon.scale(pow(-1,1),pow(-1,1)); // 反転
tile.addChild(pentagon); // グループに追加
pentagon = makePentagon(); // 五角形の生成
pentagon.scale(pow(-1,1),pow(-1,0)); // 反転
pentagon.translate(-scalar*base[0].x, scalar*base[1].y); // 五角形の位置を調整
tile.addChild(pentagon); // グループに追加
pentagon = makePentagon(); // 五角形の生成
pentagon.scale(pow(-1,0),pow(-1,1)); // 反転
pentagon.translate(scalar*base[0].x, -scalar*base[1].y); // 五角形の位置を調整
tile.addChild(pentagon); // グループに追加
}
// 格子形状に合わせたタイリングを描画する関数
void drawTiling(){
// background(255);
for (int i=0; i<lattice.length; i++){
for (int j=0; j<lattice[0].length; j++){
if( i%2 == 0 && j%2 == 0 ){
tile.resetMatrix();
tile.translate(lattice[i][j].x, lattice[i][j].y); // タイルの位置を指定
shape(tile); // タイルを描画
}
}
}
}考察
五角形によるタイリング(Type 2)は、アイソヘドラルタイリングIH27(PGG)に分類されることが分かりました。今回描いたType 2の五角形と記事IH27(PGG)で紹介した基本図形とを比較してみると、前者の五角形は後者の五角形の拡張になっていることが分かります。つまり、記事IH27(PGG)で紹介した基本図形は、今回描いたType 2の五角形において点Cと点Eが長方格子点と一致するような特別なケースであるといえそうです。