トーラス型コイル

ここでは、リサージュ図形の形の変形の例として、トーラス型コイルを考えてみます。

トーラス型コイル

ここでは、以下のようなトーラス型コイルと呼ぶ図形を作ってみます。

描き方を考える

このような図形は円（下図の赤色の円）を基準にして、この円の周りを円の接線方向に垂直になるように螺旋状にコイルを巻いていくように曲線を描くことで実現できそうです。

つまり、このような図形は\(N=2\)のリサージュ図形で実現できそうです。

\(N=2\)のリサージュ図形を復習しておきます。\(N=2\)のリサージュ図形は以下のような式で表されます。\[ x(t) = A_1 \cos ( \omega_{x,1} t + \theta_{x,1})+A_2 \cos ( \omega_{x,2} t + \theta_{x,2}) , \\ y(t) = B_1 \sin ( \omega_{y,1} t + \theta_{y,1})+ B_2 \sin ( \omega_{y,2} t + \theta_{y,2}) \]この式をみると、\(x\)方向、\(y\)方向共に2つの三角関数の重ね合わせとなっています。今回の場合に当てはめると、この重ね合わせは大きい振幅\(A_1, \ \ B_1 \)の軌道（上図の赤色の円）に対して小さい振幅\(A_2, \ \ B_2 \)の軌道（螺旋状の楕円）が付け加わるような形になると考えられます。

\(N=2\)のリサージュ図形を当てはめてみる

では、実際に当てはめてみます。今回パラメータを以下のようにとりました。\[ A_1 = B_1 = R = 120, \ \ A_2=B_2=r=60, \\ \omega_{x,1}=\omega_{y,1}=\Omega=1, \ \ \omega_{x,2}=\omega_{y,2}=\omega=120, \\ \theta_{x,1} =\theta_{y,1}=0, \ \ \theta_{x,2} = 0, \ \ \theta_{y,2} = \theta= 75 \]2つ目（小さい振幅の方）の三角関数について、その位相\(\theta_{x,2}, \ \ \theta_{y,2} \)をずらすことで楕円形になるようにしています。その結果、以下のような図形が得られました。

単純に当てはめた場合、螺旋状の部分は放射線状に拡がらず、45°傾いた楕円状の図形が円形に並べられたものになります。これは、記事「リサージュ図形（\(N=1\)）」の「位相を変化させる」のところでみたように、リサージュ曲線で描かれる楕円は基本的に45°傾いた形をしていることが反映されています。

楕円を放射線状に傾ける

今回は楕円が放射線状に並ぶようにしたいので、楕円を基準の円（\(N=2\)のリサージュ図形の大きい振幅の軌道）に垂直な形になるように回転します。

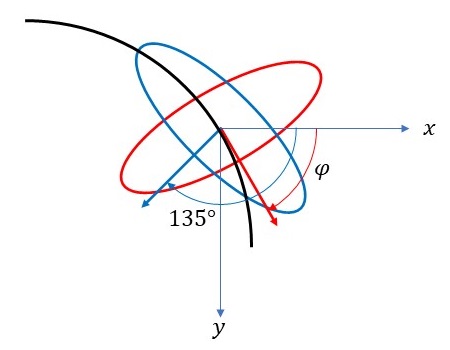
上図の青色の楕円は\(N=2\)のリサージュ図形を当てはめたときに円形にならんだ楕円のうちの１つを表しています。この青色の楕円は基本的に45°傾いた形をしているので、この楕円に垂直なベクトル（青色の矢印）は\(x\)軸の正の向きから常に135°回転した方向に向いています。ここでは、この青色の楕円を赤色の楕円のように大きな振幅の軌道（黒色の曲線）に対して放射線状になるように回転することを考えています。これは、青色の矢印が大きな振幅の軌道の接線方向（赤色の矢印）に一致するように回転させることで実現できます。つまり、大きな振幅の軌道の接線方向（赤色の矢印）が\(x\)軸の正の向きから\( \varphi \)だけ傾いているとすると、青色の楕円上のすべての点を\( \varphi-135 \)度だけ回転させることで、青色の楕円を赤色の楕円のように放射線状にすることができます。

今回の場合、大きな振幅の軌道は円となっていますので、赤色の矢印の傾き\( \varphi \)は\( \Omega t +90 \)となります。

青色の楕円上の点\( ( r \cos \omega t , r \sin (\omega t + \theta ) ) \)を楕円の中心回りに時計回りに\( \varphi-135 = \Omega t – 45 \)だけ回転させるには、\[ \begin{pmatrix} \cos (\Omega t -45 ) & -\sin (\Omega t -45 ) \\ \sin (\Omega t -45 ) & \cos (\Omega t -45 ) \end{pmatrix} \begin{pmatrix} r \cos \omega t \\ r \sin (\omega t + \theta ) \end{pmatrix} = \begin{pmatrix} r \cos \omega t \cos (\Omega t -45 ) – r \sin (\omega t + \theta ) \sin (\Omega t -45 ) \\ r \cos \omega t \sin (\Omega t -45 ) + r \sin (\omega t + \theta ) \cos (\Omega t -45 ) \end{pmatrix} \]のように座標変換することで実現することができます。この式を整理すると、\[ x(t) = \frac{r}{2} \cos \{ (\omega + \Omega )t -45 \} + \frac{r}{2} \cos \{ (\omega – \Omega )t + 45 \} + \frac{r}{2} \cos \{ (\omega + \Omega )t + \theta -45 \} – \frac{r}{2} \cos \{ (\omega – \Omega )t + \theta + 45 \} \\ y(t) = \frac{r}{2} \sin \{ (\omega + \Omega )t -45 \} + \frac{r}{2} \sin \{ (\omega – \Omega )t + 45 \} + \frac{r}{2} \sin \{ (\omega + \Omega )t + \theta -45 \} – \frac{r}{2} \sin \{ (\omega – \Omega )t + \theta + 45 \} \]となります。大きな振幅の軌道の円の座標\( ( R \cos \Omega t, R \sin \Omega t ) \)に、この式を加えると、求めたいトーラス型コイルの図形が得られます。なお、結果としてこのトーラス型コイルは\(N=5\)のリサージュ図形で実現することができることが分かります。

ソースコード

最後に、トーラス型コイルの図形を作成したときのソースコードを示しておきます。

void setup(){
  size(500,500);
  translate(width/2.0, height/2.0);
  noFill();

  int N = 2; // 項数
  // 2つ目の三角関数のy方向の位相を変化させる
  float[] r_x = {120.0, 60.0};
  float[] omega_x = {1.0, 120.0};
  float[] theta_x = {0.0, 0.0};
  float[] r_y = {120.0, 60.0};
  float[] omega_y = {1.0, 120.0};
  float[] theta_y = {0.0, 75.0}; 

  // 2つ目の円を回転させるときのパラメータ
  float omega = omega_x[0];
  float theta = -45.0;
  
  N = 5;
  float[] r2_x = {r_x[0], r_x[1]/2.0, r_x[1]/2.0, r_y[1]/2.0, -r_y[1]/2.0};
  float[] omega2_x = {omega_x[0], omega + omega_x[1], omega - omega_x[1], omega + omega_y[1], omega - omega_y[1]};
  float[] theta2_x = {theta_x[0], theta + theta_x[1], theta - theta_x[1], theta + theta_y[1], theta - theta_y[1]};
  float[] r2_y = {r_y[0], r_x[1]/2.0, r_x[1]/2.0, r_y[1]/2.0, -r_y[1]/2.0};
  float[] omega2_y = {omega_y[0], omega + omega_x[1], omega - omega_x[1], omega + omega_y[1], omega - omega_y[1]};
  float[] theta2_y = {theta_y[0], theta + theta_x[1], theta - theta_x[1], theta + theta_y[1], theta - theta_y[1]}; 

  drawLissajous(5, r2_x, omega2_x, theta2_x, r2_y, omega2_y, theta2_y);

  save("Lissajous_torus_coil.jpg");
}

// リサージュ曲線を描く関数
void drawLissajous(
  int N, // 項数
  float[] r_x, // x方向の振幅に関する配列
  float[] omega_x, // x方向の周波数に関する配列
  float[] theta_x, // x方向の位相に関する配列
  float[] r_y, // y方向の振幅に関する配列
  float[] omega_y, // y方向の周波数に関する配列
  float[] theta_y // y方向の位相に関する配列
){
  float x, y;
  int num = 10000;
 
  beginShape();
  for(int i=0; i<num; i++){
    x = 0.0;
    y = 0.0;
    for(int j=0; j<N; j++){
      x += r_x[j] * cos( omega_x[j] * radians(i*360.0/num) + radians(theta_x[j]) );
      y += r_y[j] * sin( omega_y[j] * radians(i*360.0/num) + radians(theta_y[j]) );
    }
    vertex(x,y);
  }
  endShape();
}