ここでは、書籍「マス・アート~真理、美、そして方程式~」のp.133で紹介されていた鉄の魔神という装置で描かれたリサージュ図形の再現を試みています。
鉄の魔神によるリサージュ図形の再現
今回再現したリサージュ図形は以下のようになりました。

書籍「マス・アート~真理、美、そして方程式~」のp.133の図形と比べると、ちょっと違うところもありますが、寄せることができた方ではないでしょうか。
解説
以下に、今回作成したリサージュ図形について、順番に解説していきたいと思います。
基本となるリサージュ図形
まず、図形をよく観察してみると、今回のリサージュ図形は1種類のリサージュ図形を基本として、それをコピーして回転させながら順に5つ並べたものになっていることがわかります。その1種類のリサージュ図形は次のような形をしています。

つまり、この基本となるリサージュ図形を描くことができれば、あとは並べるだけになります。
基本となるリサージュ図形を作成するための考察
さらに、この基本となるリサージュ図形をよく観察してみます。

上の図のように、楕円が見えてきます。もう少し言えば、赤色の楕円から始まり、その楕円が少しずつ長軸が短く、短軸が長くなりながら回転していき、最後に黄色の楕円に至っていることが分かります。
楕円の位相差の変化
ここで、記事「リサージュ図形(\(N=1\))」の「位相を変化させる」について思い出してみます。\( N=1 \)でのリサージュ図形の式は、以下です。
\[ x(t) = A_1 \sin ( \omega_{x,1} t + \theta_{x,1}), \ \ y(t) = B_1 \sin ( \omega_{y,1} t + \theta_{y,1}) \]
\(x(t)\)と\(y(t)\)の振幅と周波数を
\[ A_1 = B_1 = 60, \ \ \omega_{x,1} = \omega_{y,1} = 1, \ \ \theta_{x,1} = 0 \]
として、\( \theta_{y,1} \)を0°から360°まで15°ずつ変化させて描いたものが以下の図です。
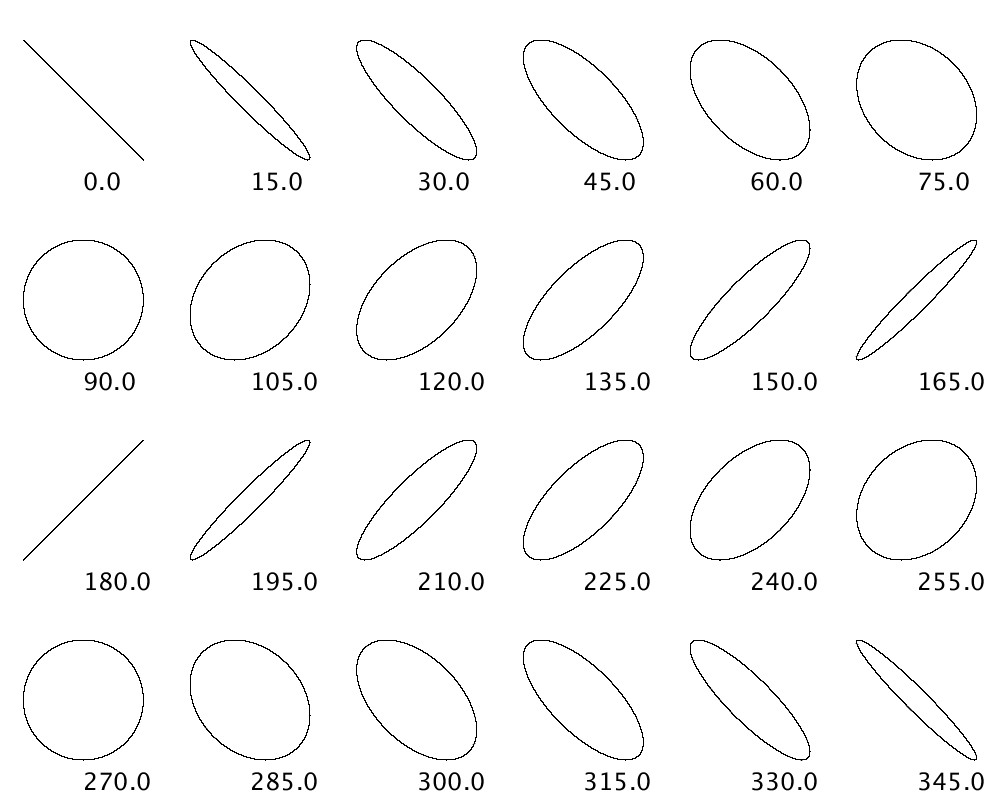
この図をみてみると、基本となるリサージュ図形は赤色の楕円が\(x(t)\)と\(y(t)\)の位相差15°の時の楕円に対応し、黄色の楕円が\(x(t)\)と\(y(t)\)の位相差75°の時の楕円に対応しているように見え、また、楕円はその位相差が15°から75°まで少しずつ変化しているように見えます。
この考察の結果を利用して、楕円をその位相差が15°から75°まで少しずつ変化するように描いてみます。今回、\( \theta_{y,1} \)を\[ \theta_{y,1} = \omega t + \theta \]のように時間変化するものとします。言い換えると、周波数\( \omega_{y,1} \)が\( \omega_{x,1} \)よりも\( \omega \)だけ大きくなることを示しています。ここでは、\[ \omega = 2.0 / 360.0, \ \ \theta = 15.0 \]にとって、楕円を30回描くと、位相差が15°から75°まで少しずつ変化するように設定しています。

この図のソースコードを示しておきます。
void setup(){
size(500,500);
translate(width/2.0, height/2.0);
noFill();
int N = 1; // 項数
// y方向の位相を変化させる
float[] r_x = {120.0};
float[] omega_x = {1.0};
float[] theta_x = {-90.0};
float[] r_y = {120.0};
float[] omega_y = {1.0+2.0/360.0};
float[] theta_y = {15.0};
PShape tile = drawLissajous(1, 30, r_x, omega_x, theta_x, r_y, omega_y, theta_y);
shape(tile);
}
// リサージュ曲線を描く関数
PShape drawLissajous(
int N, // 項数
int rotate_num, // 回転させる回数
float[] r_x, // x方向の振幅に関する配列
float[] omega_x, // x方向の周波数に関する配列
float[] theta_x, // x方向の位相に関する配列
float[] r_y, // y方向の振幅に関する配列
float[] omega_y, // y方向の周波数に関する配列
float[] theta_y // y方向の位相に関する配列
){
PShape lissajous;
float x, y;
int num = 10000;
lissajous = createShape();
lissajous.beginShape();
for(int i=0; i< rotate_num * num; i++){
x = 0.0;
y = 0.0;
for(int j=0; j<N; j++){
x += r_x[j] * cos( omega_x[j] * radians(i*360.0/num) + radians(theta_x[j]) );
y += r_y[j] * sin( omega_y[j] * radians(i*360.0/num) + radians(theta_y[j]) );
}
lissajous.vertex(x,y);
}
lissajous.endShape();
return lissajous;
}なお、ソースコードで\( x(t) \)の式を少し変えています。つまり、\[ \sin \theta = \cos \left( \theta – \frac{\pi}{2} \right) \]を利用して、\( x(t) \)の式を\( \sin \)の式から\( \cos \)の式に変更しています。
楕円の回転
基本となるリサージュ図形をもう一度眺めてみると、楕円はその大きさを変えながら少しずつ時計回り回転しているように見えます。そこで次に、図形の回転を考えてみます。
平面上の点\( (x,y) \)を原点を中心に時計回りに\( \alpha \)だけ回転させるときには、\[ \begin{pmatrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x \cos \alpha – y \sin \alpha \\ x \sin \alpha + y \cos \alpha \end{pmatrix} \]のように座標変換することで実現することができます。今回の場合、回転角度は時間に依存するので\( \alpha = \omega t \)として、座標\( (x, y) \)に\( N=1 \)でのリサージュ図形の式を入れて整理すると、\[ x(t) = \frac{A_1}{2} \cos \{ (\omega + \omega_{x,1} )t + \theta_{x,1} \} + \frac{A_1}{2} \cos \{ (\omega – \omega_{x,1} )t – \theta_{x,1} \} + \frac{B_1}{2} \cos \{ (\omega + \omega_{y,1} )t + \theta_{y,1} \} – \frac{B_1}{2} \cos \{ (\omega – \omega_{y,1} )t – \theta_{y,1} \} \\ y(t) = \frac{A_1}{2} \sin \{ (\omega + \omega_{x,1} )t + \theta_{x,1} \} + \frac{A_1}{2} \sin \{ (\omega – \omega_{x,1} )t – \theta_{x,1} \} + \frac{B_1}{2} \sin \{ (\omega + \omega_{y,1} )t + \theta_{y,1} \} – \frac{B_1}{2} \sin \{ (\omega – \omega_{y,1} )t – \theta_{y,1} \} \]となります。つまり、今回のリサージュ図形の回転は\( N=4 \)でのリサージュ図形の式として表すことができます。実際に回転を加えてみると、以下のような図形になります。

この図のソースコードを示しておきます。
void setup(){
size(500,500);
translate(width/2.0, height/2.0);
noFill();
int N = 1; // 項数
// y方向の位相を変化させる
float[] r_x = {120.0};
float[] omega_x = {1.0};
float[] theta_x = {-90.0};
float[] r_y = {120.0};
float[] omega_y = {1.0+2.0/360.0};
float[] theta_y = {15.0};
// 座標位置を回転させるときのパラメータ
float omega = 2.0/360.0;
float theta = 0.0;
N = 4;
float[] r2_x = {r_x[0]/2.0, r_x[0]/2.0, r_y[0]/2.0, -r_y[0]/2.0};
float[] omega2_x = {omega + omega_x[0], omega - omega_x[0], omega + omega_y[0], omega - omega_y[0]};
float[] theta2_x = {theta + theta_x[0], theta - theta_x[0], theta + theta_y[0], theta - theta_y[0]};
float[] r2_y = {r_x[0]/2.0, r_x[0]/2.0, r_y[0]/2.0, -r_y[0]/2.0};
float[] omega2_y = {omega + omega_x[0], omega - omega_x[0], omega + omega_y[0], omega - omega_y[0]};
float[] theta2_y = {theta + theta_x[0], theta - theta_x[0], theta + theta_y[0], theta - theta_y[0]};
PShape tile = drawLissajous(4, 30, r2_x, omega2_x, theta2_x, r2_y, omega2_y, theta2_y);
shape(tile);
}
// リサージュ曲線を描く関数
PShape drawLissajous(
int N, // 項数
int rotate_num, // 回転させる回数
float[] r_x, // x方向の振幅に関する配列
float[] omega_x, // x方向の周波数に関する配列
float[] theta_x, // x方向の位相に関する配列
float[] r_y, // y方向の振幅に関する配列
float[] omega_y, // y方向の周波数に関する配列
float[] theta_y // y方向の位相に関する配列
){
PShape lissajous;
float x, y;
int num = 10000;
lissajous = createShape();
lissajous.beginShape();
for(int i=0; i< rotate_num * num; i++){
x = 0.0;
y = 0.0;
for(int j=0; j<N; j++){
x += r_x[j] * cos( omega_x[j] * radians(i*360.0/num) + radians(theta_x[j]) );
y += r_y[j] * sin( omega_y[j] * radians(i*360.0/num) + radians(theta_y[j]) );
}
lissajous.vertex(x,y);
}
lissajous.endShape();
return lissajous;
}摩擦を考慮する
上記で楕円を回転させることで、その形が基本となるリサージュ図形に近づいてきましたが、まだ楕円の大きさに違いがあります。これは、鉄の魔神という装置がペンで実際の紙上にリサージュ曲線を描くものであることが関連していると考えられます。つまり、紙とペンの間に摩擦抵抗が生じるため、リサージュ曲線の振幅が時間が経過とともに少しずつ減衰していることが考えられます。そのため、振幅が時間的に減衰することを表す項\( \exp ( – k t ) \)を振幅にかけます。結果として、基本となるリサージュ図形を描くことができます。ここまでのソースコードを示しておきます。
void setup(){
size(500,500);
translate(width/2.0, height/2.0);
noFill();
int N = 1; // 項数
// y方向の位相を変化させる
float[] r_x = {120.0};
float[] omega_x = {1.0};
float[] theta_x = {-90.0};
float[] r_y = {120.0};
float[] omega_y = {1.0+2.0/360.0};
float[] theta_y = {15.0};
// 座標位置を回転させるときのパラメータ
float omega = 2.0/360.0;
float theta = 0.0;
N = 4;
float[] r2_x = {r_x[0]/2.0, r_x[0]/2.0, r_y[0]/2.0, -r_y[0]/2.0};
float[] omega2_x = {omega + omega_x[0], omega - omega_x[0], omega + omega_y[0], omega - omega_y[0]};
float[] theta2_x = {theta + theta_x[0], theta - theta_x[0], theta + theta_y[0], theta - theta_y[0]};
float[] r2_y = {r_x[0]/2.0, r_x[0]/2.0, r_y[0]/2.0, -r_y[0]/2.0};
float[] omega2_y = {omega + omega_x[0], omega - omega_x[0], omega + omega_y[0], omega - omega_y[0]};
float[] theta2_y = {theta + theta_x[0], theta - theta_x[0], theta + theta_y[0], theta - theta_y[0]};
PShape tile = drawLissajous(4, 30, r2_x, omega2_x, theta2_x, r2_y, omega2_y, theta2_y);
shape(tile);
}
// リサージュ曲線を描く関数
PShape drawLissajous(
int N, // 項数
int rotate_num, // 回転させる回数
float[] r_x, // x方向の振幅に関する配列
float[] omega_x, // x方向の周波数に関する配列
float[] theta_x, // x方向の位相に関する配列
float[] r_y, // y方向の振幅に関する配列
float[] omega_y, // y方向の周波数に関する配列
float[] theta_y // y方向の位相に関する配列
){
PShape lissajous;
float x, y;
int num = 10000;
lissajous = createShape();
lissajous.beginShape();
for(int i=0; i< rotate_num * num; i++){
x = 0.0;
y = 0.0;
for(int j=0; j<N; j++){
x += r_x[j] * exp(-0.00006 * i * 360.0/num ) * cos( omega_x[j] * radians(i*360.0/num) + radians(theta_x[j]) );
y += r_y[j] * exp(-0.00006 * i * 360.0/num ) * sin( omega_y[j] * radians(i*360.0/num) + radians(theta_y[j]) );
}
lissajous.vertex(x,y);
}
lissajous.endShape();
return lissajous;
}ソースコード
基本となるリサージュ図形が描けると、あとはこの図形をコピーして角度をずらしながら描いていけば、鉄の魔神が描いたという図形を再現することができます。最後に、その図形を再現するためのソースコードを示しておきます。
void setup(){
size(500,500);
translate(width/2.0, height/2.0);
noFill();
int N = 1; // 項数
// y方向の位相を変化させる
float[] r_x = {120.0};
float[] omega_x = {1.0};
float[] theta_x = {-90.0};
float[] r_y = {120.0};
float[] omega_y = {1.0+2.0/360.0};
float[] theta_y = {15.0};
// 座標位置を回転させるときのパラメータ
float omega = 2.0/360.0;
float theta = 0.0;
N = 4;
float[] r2_x = {r_x[0]/2.0, r_x[0]/2.0, r_y[0]/2.0, -r_y[0]/2.0};
float[] omega2_x = {omega + omega_x[0], omega - omega_x[0], omega + omega_y[0], omega - omega_y[0]};
float[] theta2_x = {theta + theta_x[0], theta - theta_x[0], theta + theta_y[0], theta - theta_y[0]};
float[] r2_y = {r_x[0]/2.0, r_x[0]/2.0, r_y[0]/2.0, -r_y[0]/2.0};
float[] omega2_y = {omega + omega_x[0], omega - omega_x[0], omega + omega_y[0], omega - omega_y[0]};
float[] theta2_y = {theta + theta_x[0], theta - theta_x[0], theta + theta_y[0], theta - theta_y[0]};
PShape tile = drawLissajous(4, 30, r2_x, omega2_x, theta2_x, r2_y, omega2_y, theta2_y);
for(int i=0; i<5; i++){
tile.resetMatrix();
tile.rotate(2.0 /5.0 * PI * i);
tile.translate( cos(radians(-45.0)) * width /6.0, sin(radians(-45.0)) * width /6.0 );
shape(tile);
}
save("Lissajous_IronGenie.jpg");
}
// リサージュ曲線を描く関数
PShape drawLissajous(
int N, // 項数
int rotate_num, // 回転させる回数
float[] r_x, // x方向の振幅に関する配列
float[] omega_x, // x方向の周波数に関する配列
float[] theta_x, // x方向の位相に関する配列
float[] r_y, // y方向の振幅に関する配列
float[] omega_y, // y方向の周波数に関する配列
float[] theta_y // y方向の位相に関する配列
){
PShape lissajous;
float x, y;
int num = 10000;
lissajous = createShape();
lissajous.beginShape();
for(int i=0; i< rotate_num * num; i++){
x = 0.0;
y = 0.0;
for(int j=0; j<N; j++){
x += r_x[j] * exp(-0.00006 * i * 360.0/num ) * cos( omega_x[j] * radians(i*360.0/num) + radians(theta_x[j]) );
y += r_y[j] * exp(-0.00006 * i * 360.0/num ) * sin( omega_y[j] * radians(i*360.0/num) + radians(theta_y[j]) );
}
lissajous.vertex(x,y);
}
lissajous.endShape();
return lissajous;
}